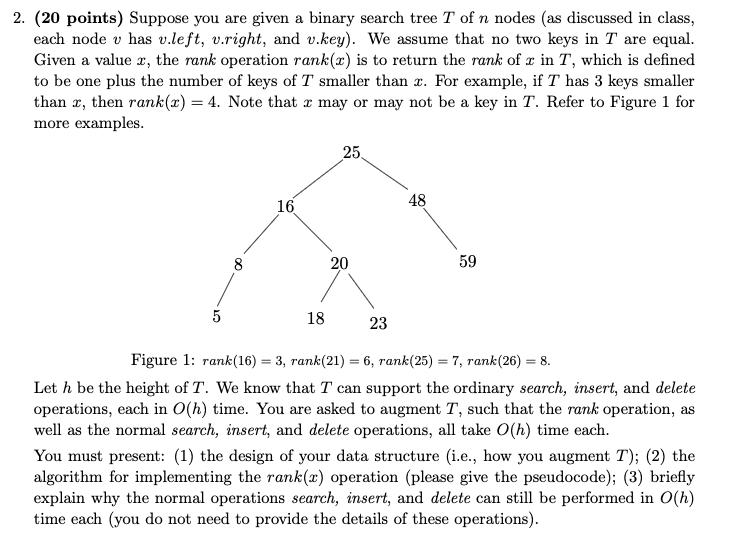
2. (20 points) Suppose you are given a binary search tree T of n nodes (as discussed in class, each node v has v.left, v.right, and v.key). We assume that no two keys in T are equal. Given a value x, the rank operation rank(I) is to return the rank of u in T, which is defined to be one plus the number of keys of T smaller than 2. For example, if T has 3 keys smaller than x, then rank(x) = 4. Note that 2 may or may not be a key in T. Refer to Figure 1 for more examples. 25. 16 48 8 20 59 5 18 23 Figure 1: rank(16) = 3, rank(21) = 6, rank(25) = 7, rank(26) = 8. Let h be the height of T. We know that T can support the ordinary search, insert, and delete operations, each in 0(h) time. You are asked to augment T, such that the rank operation, as well as the normal search, insert, and delete operations, all take O(h) time each. You must present: (1) the design of your data structure (i.e., how you augment T); (2) the algorithm for implementing the rank(x) operation (please give the pseudocode); (3) briefly explain why the normal operations search, insert, and delete can still be performed in 0(h) time each (you do not need to provide the details of these operations)