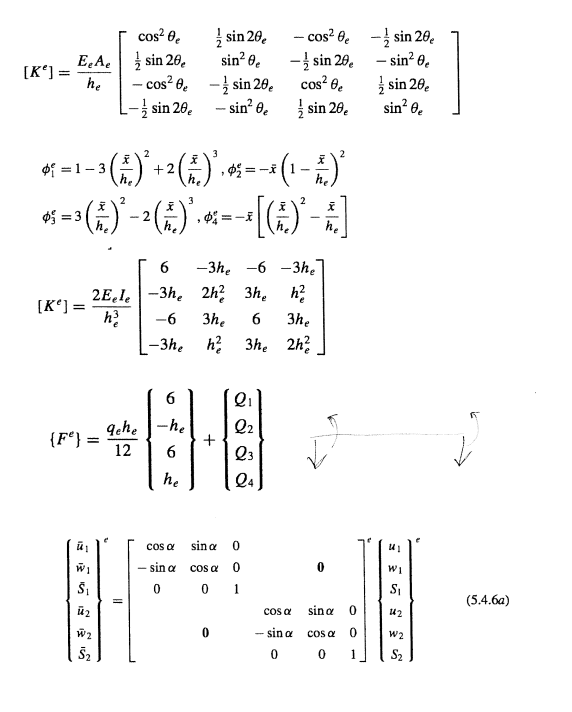
2. (20 points) The heat conduction problem in a thin circular plate is governed by: d a (rar) + dr dT dr +rs 0, 0 < r < R = essential boundary condition: T(r = R) = To, dT natural boundary condition: = 0, dr (1) (2) (3) (4) where R is the total radius of the plate, s is the heat source per unit length along the plate radius, T is the temperature and k is the conductivity. The given problem data consists of R, To, and the functions k(r) and s(r). Derive the weak form for this problem. cos Be sin 20 -cos sin 20 E.A sin 20 sin e sin 20 sin 0. [K]= he - cos L-sin 20 sin 20 cos Be sin 20 - sin 0 sin 20 sin e =1-3 = 3 2 2 +2 3 =-x 2 (1. - x =-x he 6 -3he -6 -3he 2Eele -3he 2h2 3h, h [Ke] = h -6 3he 6 3he -3he h 3he 2h2 6 gehe -he Q2 {Fe} = + 12 6 23 he 24 cos sina 0 W1 - sin a cosa 0 S 001 cos sina 0 W2 0 - sin a cos a 52 00 F WI S (5.4.6a) 142 WA 1 S