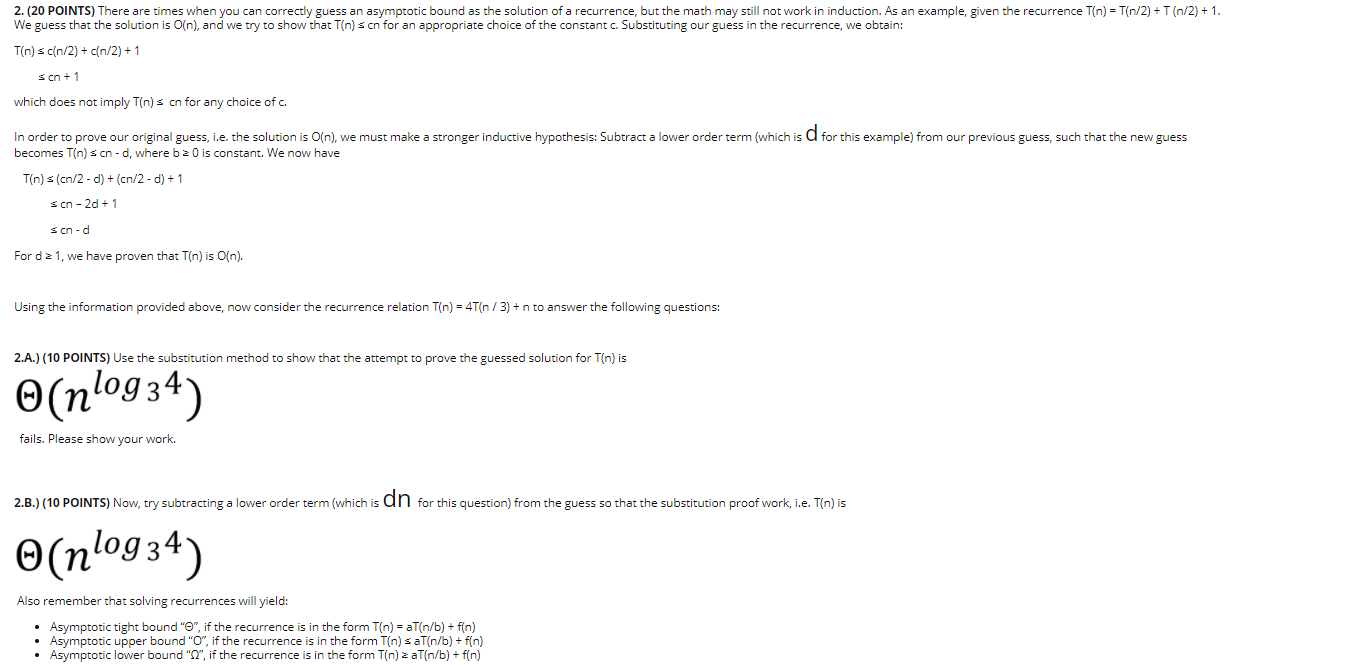
2. (20 POINTS) There are times when you can correctly guess an asymptotic bound as the solution of a recurrence, but the math may still not work in induction. As an example, given the recurrence T(n) = Tn/2) +T (n/2) + 1. We guess that the solution is O(n), and we try to show that T(n) son for an appropriate choice of the constant c. Substituting our guess in the recurrence, we obtain: T(n): cn/2) + cn/2 + 1 son +1 which does not imply T(n) s cn for any choice of c. In order to prove our original guess, i.e. the solution is O(n), we must make a stronger inductive hypothesis: Subtract a lower order term (which is d for this example) from our previous guess, such that the new guess becomes Tin) scn-d, where bois constant. We now have Tin) s (cn/2 - d) + (cn/2 - d) + 1 son - 2d + 1 scn-d For d = 1, we have proven that T(n) is O(n). Using the information provided above, now consider the recurrence relation T(n) = 4T(n /3) +n to answer the following questions: 2.A.) (10 POINTS) Use the substitution method to show that the attempt to prove the guessed solution for T(n) is (nlog34) fails. Please show your work. 2.B.) (10 POINTS) Now, try subtracting a lower order term (which is dn for this question) from the guess so that the substitution proof work, i.e. Tin) is (nlog34) Also remember that solving recurrences will yield: Asymptotic tight bound "O", if the recurrence is in the form T(n) = aT(n/b) + f(n) Asymptotic upper bound "O", if the recurrence is in the form T(n) s aT(n/b) + f(n) Asymptotic lower bound "O", if the recurrence is in the form T(n) 2 aT(n/b) + f(n)