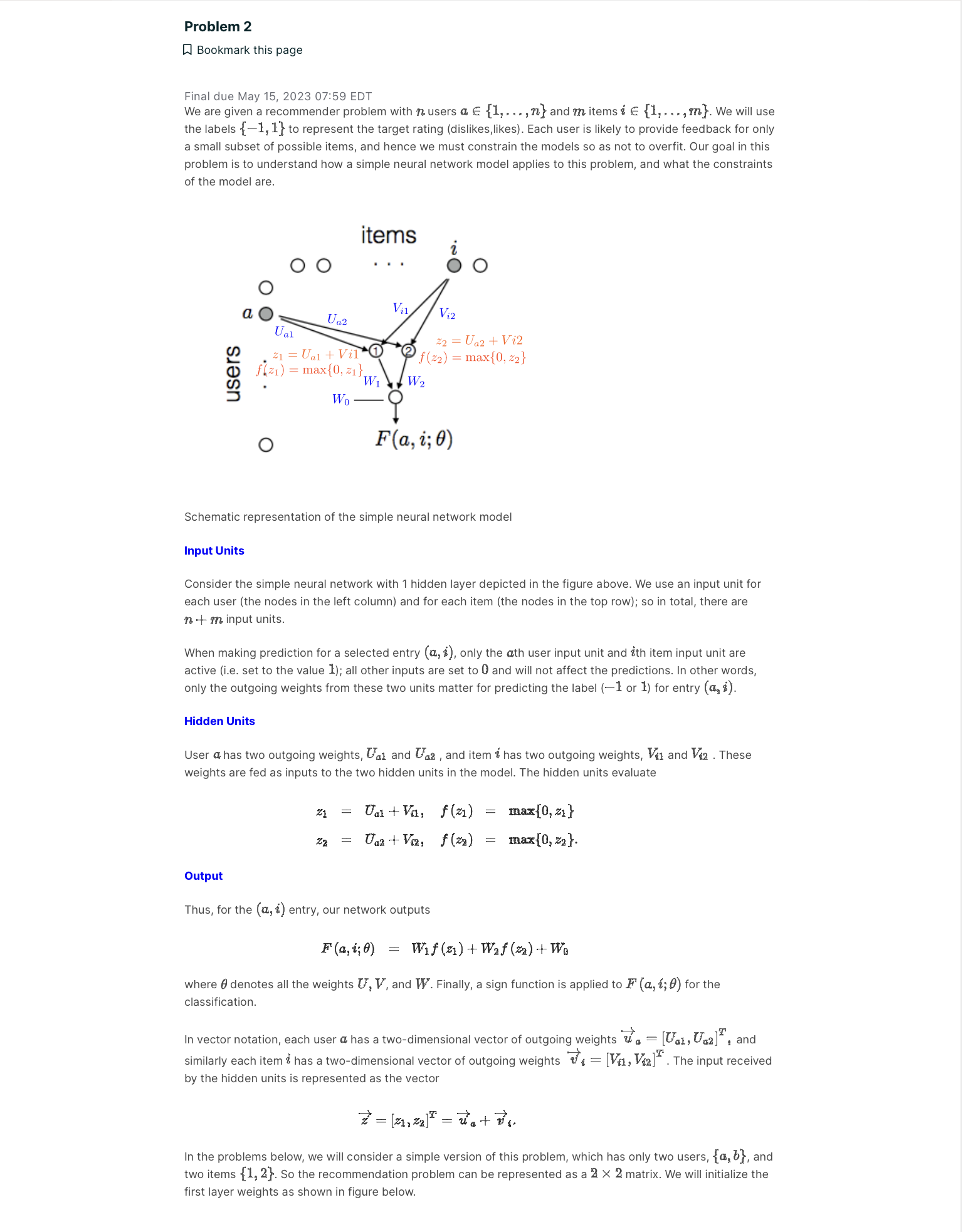
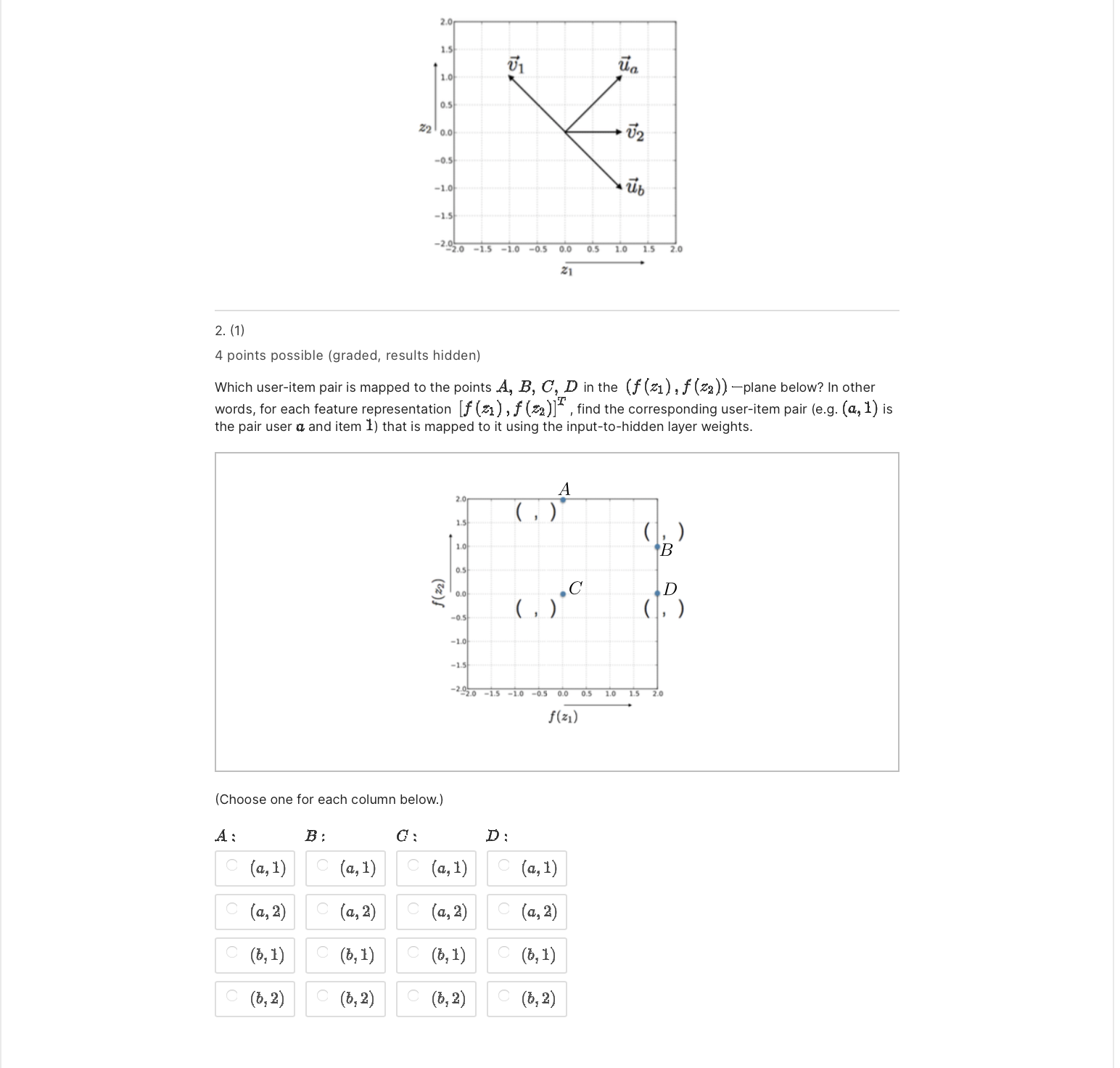
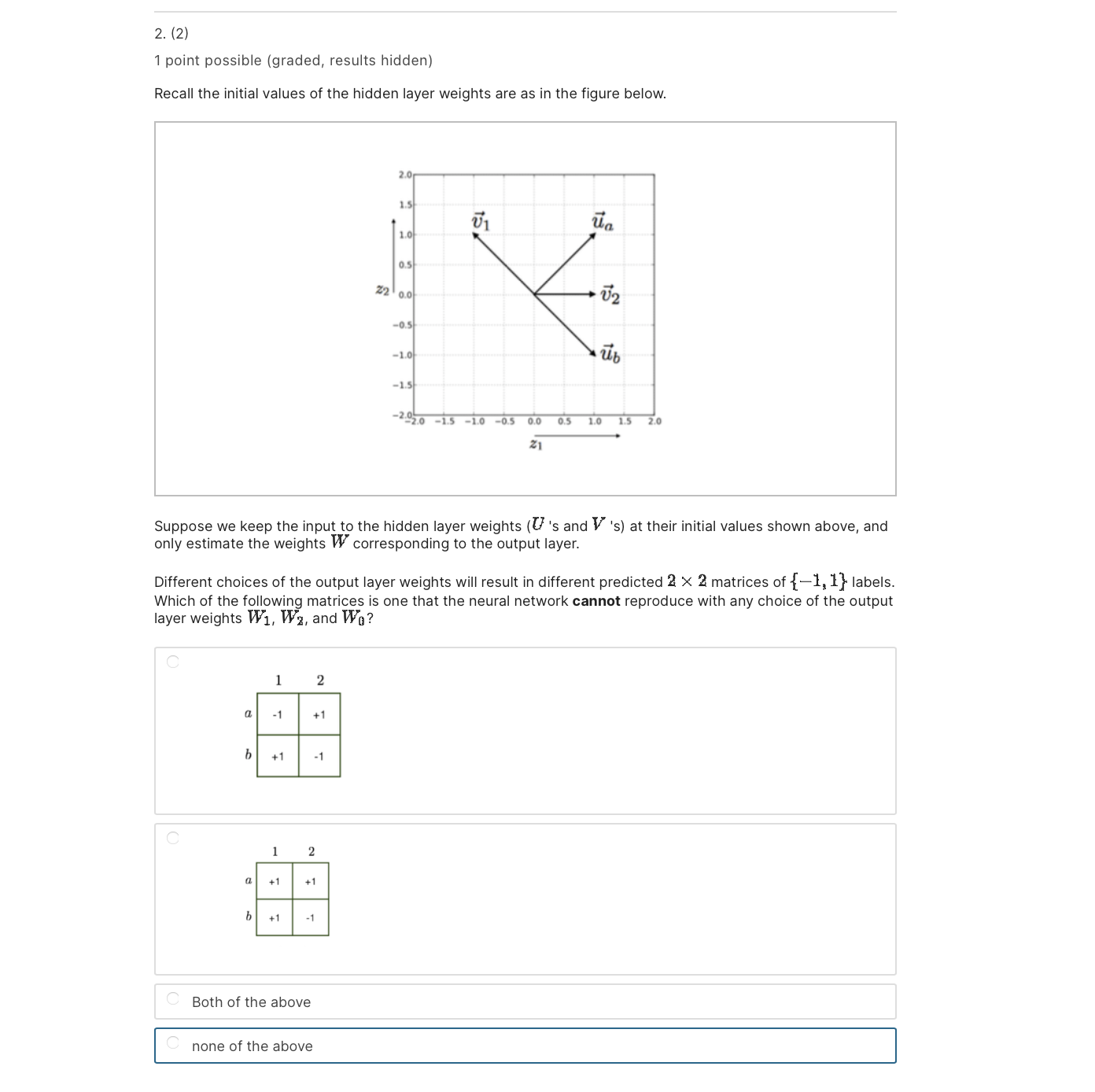
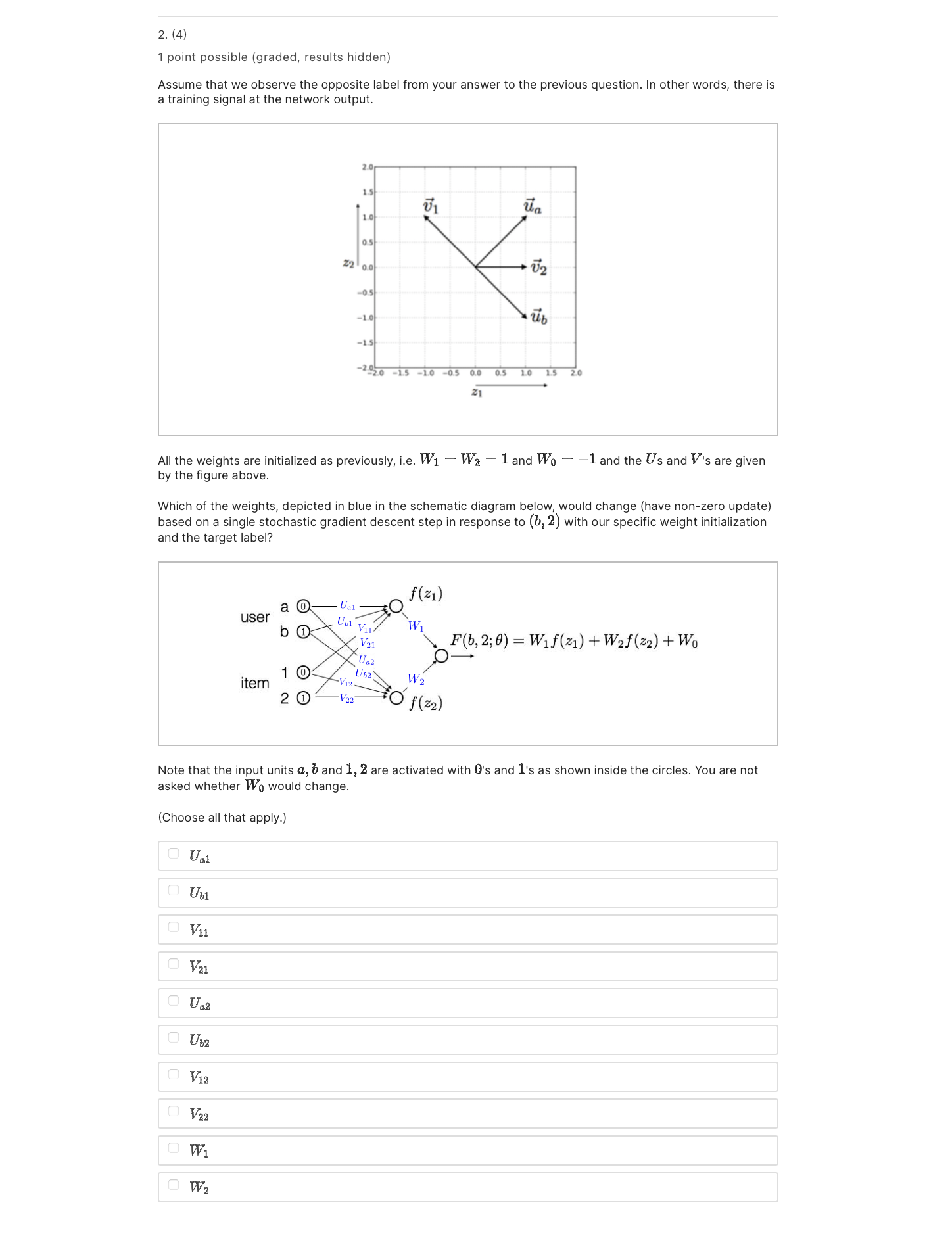
2. (3] 1 point possible (graded, results hidden) Learning a new representation for examples (hidden layer activations) is always harder than learning the linear classifier operating on that representation. In neural networks. the representation is learned together with the end classifier using stochastic gradient descent. We initialize the output layer weights as W1 = W; = 1 and Wu = 1. Assume that all the weights are initialized as previously: n 15 to as Z: on so: to -13 .39 a .qa IS do 05 00 03 [0 IS 2n . 3| What is the class label +1 or 1 that the network would predict in response to (5,2) (user 6, item 2]? You have used 0 of 3 attempts Save Problem 2 El Bookmark this page Final due May 15, 2023 07:59 EDT We are given a recommender problem with in. users a. E {1, . .. ,} and m itemsi E {1,. . . ,m}. We will use the labels {#1, 1} to represent the target rating (dislikes,likes). Each user is likely to provide feedback for only a small subset of possible items, and hence we must constrain the models so as not to overfit. Our goal in this problem is to understand how a simple neural network model applies to this problem, and what the constraints of the model are. users Schematic representation of the simple neural network model Input Units Consider the simple neural network with 1 hidden layer depicted in the figure above. We use an input unit for each user [the nodes in the left column) and for each item (the nodes in the top row); so in total, there are n + m input units. When making prediction for a selected entry (0., i), only the nth user input unit and ith item input unit are active (Le. set to the value 1); all other inputs are set to I} and will not affect the predictions. In other words, only the outgoing weights from these two units matter for predicting the label (1 or 1) for entry (:1, 3'). Hidden Units User a has two outgoing weights, an and U52 , and item 17 has two outgoing weights, \"1 and V1: . These weights are fed as inputs to the two hidden units in the model. The hidden units evaluate 21 = rind-W1: J'CJIJ = M{U,2:1} 2: : Uaa+Waa J'U'a] max{0, 23}. Output Thus, for the (an?) entry, our network outputs F(,'i;9) : W1f(31)+W:f(53)+Wg where 6 denotes all the weights U, V, and W. Finally, a sign function is applied to F (a, i; 9) for the classification. 12" In vector notation, each user a has a twodimensional vector of outgoing weights u a = [Ual, U52 , and , , , - , T , Similarly each item i has a twodimensional vector of outgoing weights 7: = ['41, Via] . The input received by the hidden units is represented as the vector l- .I' =1\"; 13;. I- :1" z = [zl'i $1] + In the problems below, we will consider a simple version of this problem, which has only two users, {11,13}, and two items {1, 2}. So the recommendation problem can be represented as a 2 X 2 matrix. We will initialize the first layer weights as shown in figure below. U1 Ua -0.5 -1.0 -1.5 -2020 -1.5 -1.0 -0.5 0.0 0.5 1.0 2. (1) 4 points possible (graded, results hidden) Which user-item pair is mapped to the points A, B, C, D in the (f (z1) , f (z2 )) -plane below? In other words, for each feature representation If (z1 ) , f (z2)] , find the corresponding user-item pair (e.g. (a, 1) is the pair user a and item 1) that is mapped to it using the input-to-hidden layer weights. B f(z2) -1.0 -1.5 -2020 -1.5 -1.0 -05 0.0 05 1.0 1.5 2.0 f(z1) (Choose one for each column below.) D : A : B : C (a, 1) C (a, 1) C ( a, 1) C (a, 1) C (a, 2) C (a, 2) (a, 2) (a, 2) C (b, 1) C (6, 1) C (b, 1) C (b, 1) C (b, 2) C (b, 2) C (b, 2) C (b, 2)2. (2) 1 point possible (graded, results hidden) Recall the initial values of the hidden layer weights are as in the figure below. 20 1.5 U1 It\" 10 (H 22 M 5'2 ens do ab -13 "'93.: 7\" do "as 00 05 to Is 2n Suppose we keep the input to the hidden layer weights (U 's and V 's] at their initial values shown above, and only estimate the weights W corresponding to the output layer. Different choices of the output layer weights will result in different predicted 2 X 2 matrices of {#1, 1} labels. Which of the following matrices is one that the neural network cannot reproduce with any choice of the output layer weights W1, W3, and Wu? 1 2 Both of the above none of the above 2. (4) 1 point possible (graded, results hidden) Assume that we observe the opposite label from your answer to the previous question. In other words, there is a training signal at the network output. In 15 \"1 \"a 10 05 22 0,, 172 05 40 ab '15 720)0 l -ID -! (ID 01 I0 15 In In All the weights are initialized as previously, i.e. W1 = W: = 1 and We = 1 and the Us and V's are given by the figure above. Which of the weights, depicted in blue in the schematic diagram below, would change (have nonzero update) based on a single stochastic gradient descent step in response to (b, 2) with our specific weight initialization and the target label? Note that the input units a, b and 1, 2 are activated with 0's and is as shown inside the circles. You are not asked whether Wu would change. (Choose all that apply.) Ural