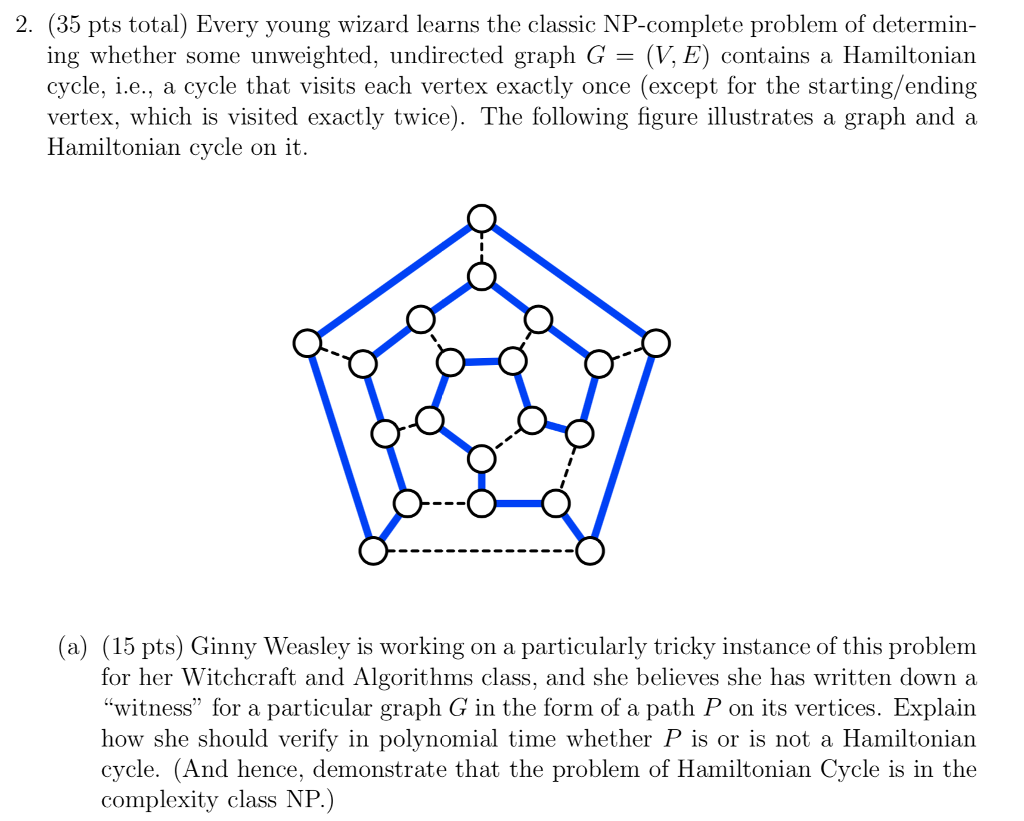
2. (35 pts total) Every young wizard learns the classic NP-complete problem of determin- ing whether some unweighted, undirected graph G -(V, E) contains a Hamiltonian cycle, i.e., a cycle that visits each vertex exactly once (except for the starting/ending vertex, which is visited exactly twice). The following figure illustrates a graph and a Hamiltonian cycle on it (a) (15 pts) Ginny Weasley is working on a particularly tricky instance of this problem for her Witchcraft and Algorithms class, and she believes she has written down a "witness" for a particular graph G in the form of a path P on its vertices. Explain how she should verify in polynomial time whether P is or is not a Hamiltonian cycle. (And hence, demonstrate that the problem of Hamiltonian Cycle is in the complexity class NP.)