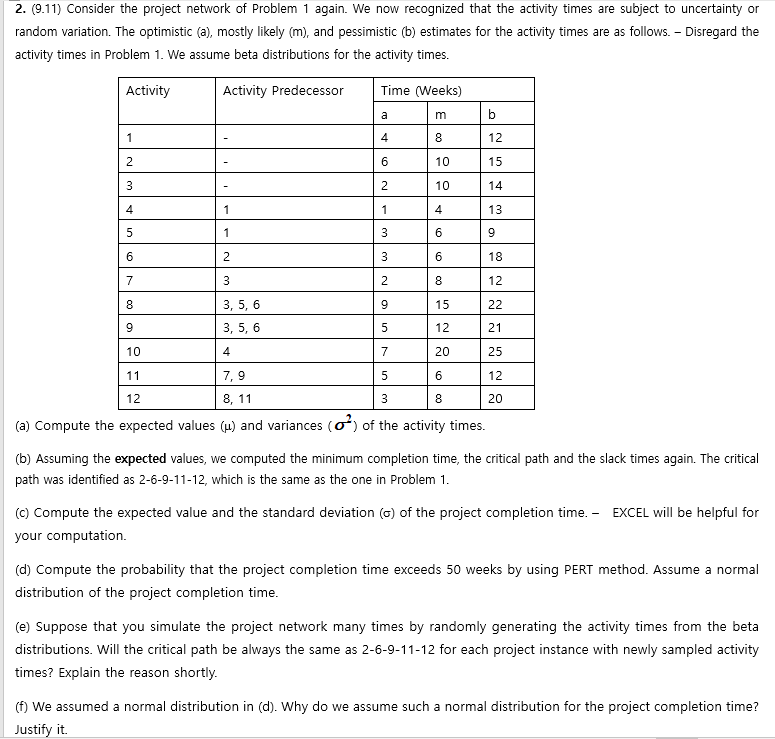
Question: 2. (9.11) Consider the project network of Problem 1 again. We now recognized that the activity times are subject to uncertainty or random variation. The
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


