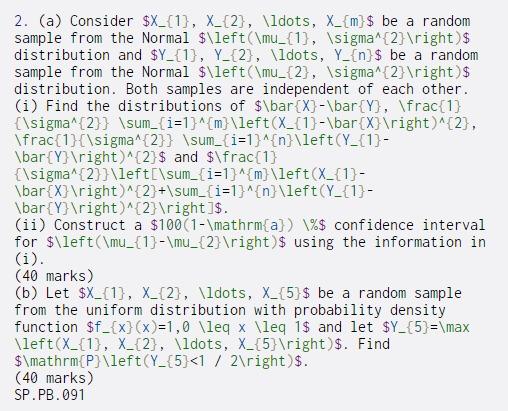
2. (a) Consider $X_{1}, X_{2}, \ldots, X_{m}$ be a random sample from the Normal $\left(\mu_{1}, \sigma^{2} ight) $ distribution and $Y_{1}, Y_{2}, \ldots, Y_{n}$ be a random sample from the Normal $\left(\mu_{2}, \sigma^{2} ight) $ distribution. Both samples are independent of each other. (i) Find the distributions of $\bar{X}-\bar{Y}, \frac{1} {\sigma^{2}} \sum_{i=1}^{m}\left(x_{1}-\bar{X} ight)^{2}, \frac{1}{\sigma^{2}} \sum_{i=1}^{n}\left(Y_{1}- \bar{Y} ight)^{2}$ and $\frac{1} {\sigma^{2}}\left\sum_{i=1}^{m}\left(x_{1}- \bar{X} ight)^{2}+\sum_{i=1}^{n}\left(Y_{1}- \bar{Y} ight)^{2} ight ]$. (ii) Construct a $100(1-\mathrm{a}) \%$ confidence interval for $\left(\mu_{1}-\mu_{2} ight)$ using the information in (i). (40 marks) (b) Let $X_{1}, X_{2}, \ldots, X_{5}$ be a random sample from the uniform distribution with probability density function $f_{x}(x)=1,0 \leq x \leq 1$ and let $Y_{5}=\max \left(x_{1}, X_{2}, \ldots, X_{5} ight)$. Find $\mathrm{P}\left(Y_{5}