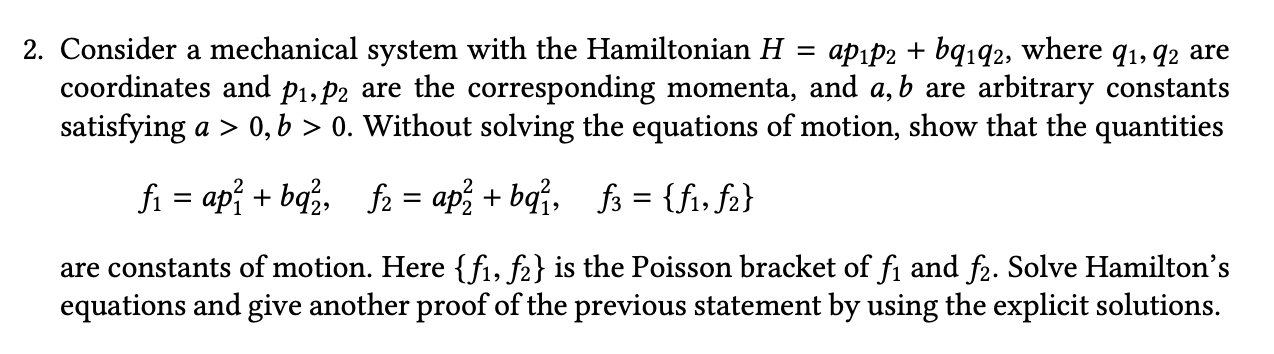
2. Consider a mechanical system with the Hamiltonian H = ap1p2 + bq192, where 91, 92 are coordinates and p1, p2 are the corresponding momenta, and a, b are arbitrary constants satisfying a > 0,6 > 0. Without solving the equations of motion, show that the quantities fi = ap + bqz, f2 = ap + bq, f3 = {fi, f2} are constants of motion. Here {fi, f2} is the Poisson bracket of f and f2. Solve Hamilton's equations and give another proof of the previous statement by using the explicit solutions. 2. Consider a mechanical system with the Hamiltonian H = ap1p2 + bq192, where 91, 92 are coordinates and p1, p2 are the corresponding momenta, and a, b are arbitrary constants satisfying a > 0,6 > 0. Without solving the equations of motion, show that the quantities fi = ap + bqz, f2 = ap + bq, f3 = {fi, f2} are constants of motion. Here {fi, f2} is the Poisson bracket of f and f2. Solve Hamilton's equations and give another proof of the previous statement by using the explicit solutions