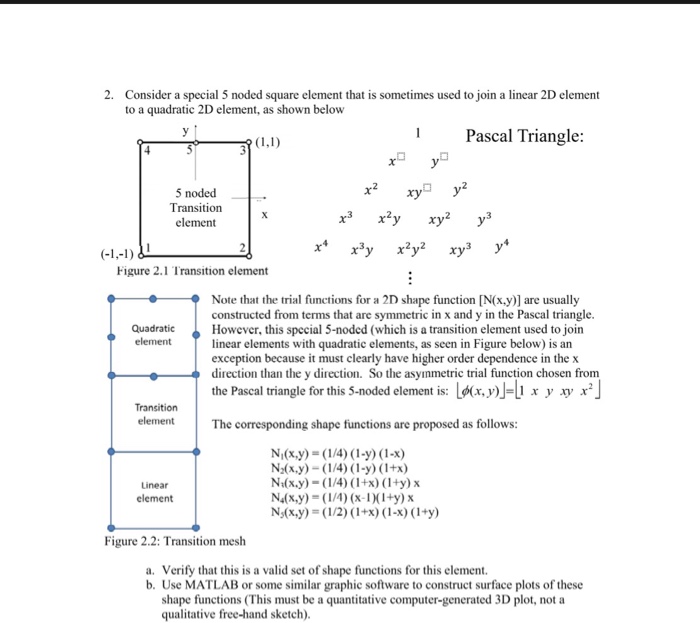
2. Consider a special 5 noded square element that is sometimes used to join a linear 2D element to a quadratic 2D element, as shown below Pascal Triangle: 5 noded Transition element xyy 1,-1) Figure 2.1 Transition element Note that the trial functions for a 2D shape function [N(x.y)] are usually constructed from terms that are symmetric in x and y in the Pascal triangle However, this special 5-noded (which is a transition element used to join linear elements with quadratic elements, as seen in Figure below) is an exception because it must clearly have higher order dependence in the x direction than the y direction. So the asynmetric trial function chosen from the Pascal triangle for this 5-noded element is: | (x, y)- 1 x v xv x2 | element elementThe corresponding shape functions are proposed as follows: Ndx.y) = ( 1 /4) ( 1-y) ( 14) Linear element N(x,y) (1/4 (x-DI+y) x Ndx.y) = ( 1 /2) ( 1 +x) ( 1-X) ( 1+y) Figure 2.2: Transition mesh a. Verify that this is a valid set of shape functions for this element. b. Use MATLAB or some similar graphic software to construct surface plots of these shape functions (This must be a quantitative computer-generated 3D plot, not a qualitative free-hand sketch). 2. Consider a special 5 noded square element that is sometimes used to join a linear 2D element to a quadratic 2D element, as shown below Pascal Triangle: 5 noded Transition element xyy 1,-1) Figure 2.1 Transition element Note that the trial functions for a 2D shape function [N(x.y)] are usually constructed from terms that are symmetric in x and y in the Pascal triangle However, this special 5-noded (which is a transition element used to join linear elements with quadratic elements, as seen in Figure below) is an exception because it must clearly have higher order dependence in the x direction than the y direction. So the asynmetric trial function chosen from the Pascal triangle for this 5-noded element is: | (x, y)- 1 x v xv x2 | element elementThe corresponding shape functions are proposed as follows: Ndx.y) = ( 1 /4) ( 1-y) ( 14) Linear element N(x,y) (1/4 (x-DI+y) x Ndx.y) = ( 1 /2) ( 1 +x) ( 1-X) ( 1+y) Figure 2.2: Transition mesh a. Verify that this is a valid set of shape functions for this element. b. Use MATLAB or some similar graphic software to construct surface plots of these shape functions (This must be a quantitative computer-generated 3D plot, not a qualitative free-hand sketch)