$2.$ Cournot competition

pls try to do the graph also

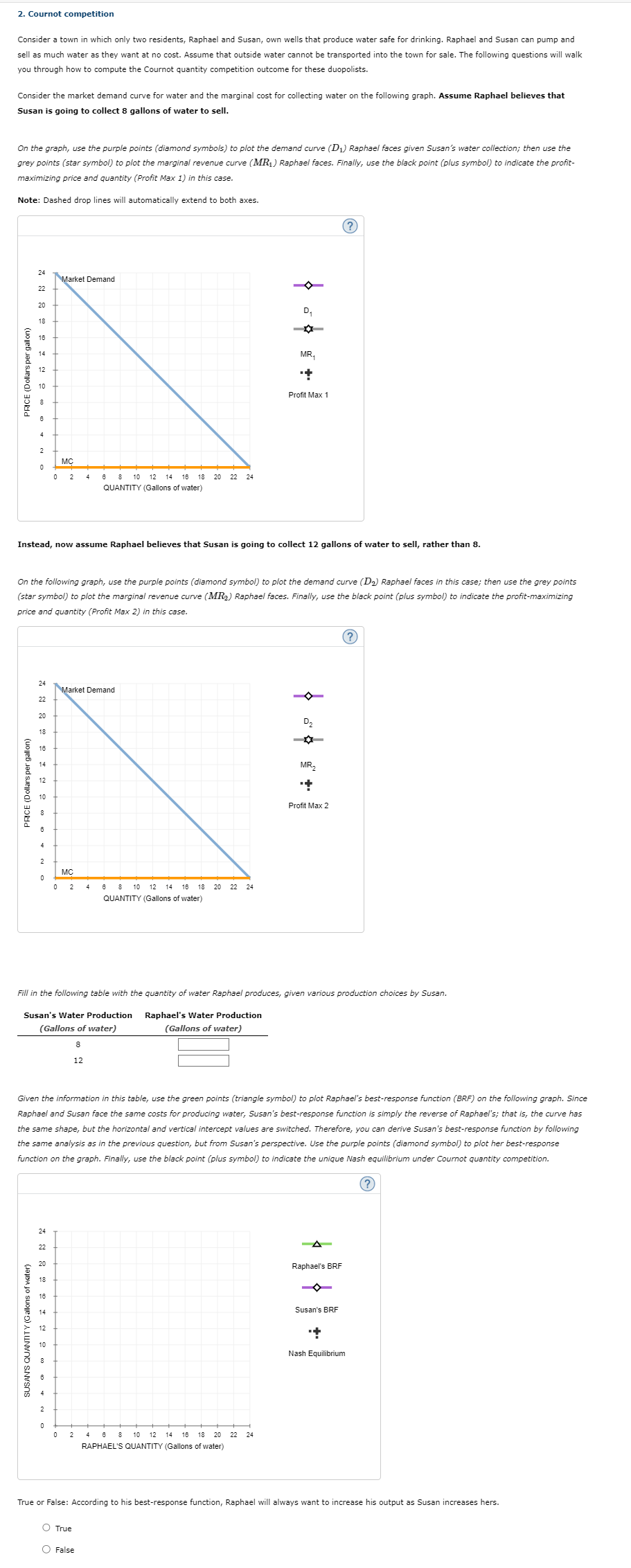
Consider a town in which only two residents, Raphael and Susan, own wells that produce water safe for drinking. Raphael and Susan can pump and sell as much water as they want at no cost$.$ Assume that outside water cannot be transported into the town for sale. The following questions will walk you through how to compute the Cournot quantity competition outcome for these duopolists.

Consider the market demand curve for water and the marginal cost for collecting water on the following graph. Assume Raphael believes that Susan is going to collect $\backslash (\backslash$mathbf$\{8\}\backslash )$ gallons of water to sell.

On the graph, use the purple points $($diamond symbols$)$ to plot the demand curve $(\backslash ($ D$\_\{1\}\backslash ))$ Raphael faces given Susan's water collection; then use the grey points $($star symbol$)$ to plot the marginal revenue curve $(\backslash ($ M R$\_\{1\}\backslash ))$ Raphael faces. Finally, use the black point $($plus symbol$)$ to indicate the profitmaximizing price and quantity $($Profit Max $1)$ in this case.

Note: Dashed drop lines will automatically extend to both axes.

Instead, now assume Raphael believes that Susan is going to collect $\backslash (\backslash$mathbf$\{12\}\backslash )$ gallons of water to sell, rather than $\backslash (\backslash$mathbf$\{8\}\backslash ).$

On the following graph, use the purple points $($diamond symbol$)$ to plot the demand curve $(\backslash ($ D$\_\{2\}\backslash ))$ Raphael faces in this case; then use the grey points $($star symbol$)$ to plot the marginal revenue curve $(\backslash ($ M R$\_\{2\}\backslash ))$ Raphael faces. Finally, use the black point $($plus symbol$)$ to indicate the profit$-$maximizing price and quantity $($Profit Max $2)$ in this case.

Fill in the following table with the quantity of water Raphael produces, given various production choices by Susan.

Given the information in this table, use the green points $($triangle symbol$)$ to plot Raphael's best$-$response function $($BRF$)$ on the following graph. Since Raphael and Susan face the same costs for producing water, Susan's best$-$response function is simply the reverse of Raphael's; that is$,$ the curve has the same shape, but the horizontal and vertical intercept values are switched. Therefore, you can derive Susan's best$-$response function by following the same analysis as in the previous question, but from Susan's perspective. Use the purple points $($diamond symbol$)$ to plot her best$-$response function on the graph. Finally, use the black point $($plus symbol$)$ to indicate the unique Nash equilibrium under Cournot quantity competition.TrueFalse