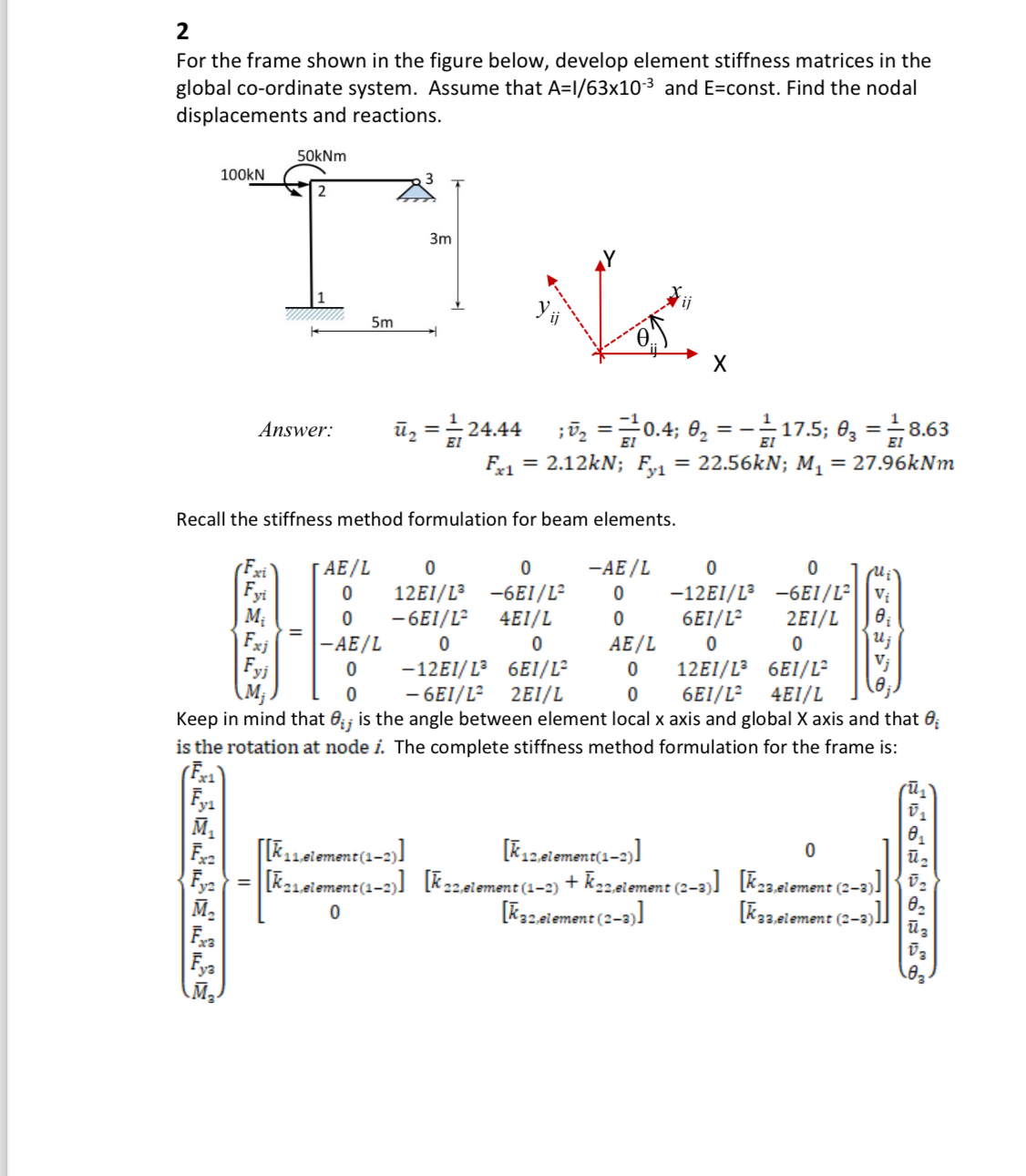
$2$

For the frame shown in the figure below, develop element stiffness matrices in the global co$-$ordinate system. Assume that $A=\frac{1}{63}{10}^{-3}$ and $E=$ const. Find the nodal displacements and reactions.

Answer:

$\frac{?}{\text{b}\text{a}\text{r}}(u{)}_2=\frac{1}{EI}24\mathrm{.}44,\frac{\text{;}}{b}ar(v{)}_2=\frac{-1}{EI}0\mathrm{.}4$;${}_2=-\frac{1}{EI}17\mathrm{.}5$;${}_3=\frac{1}{EI}8\mathrm{.}63$

$F_{x1}=2\mathrm{.}12kN$;$F_{y1}=22\mathrm{.}56kN$;$M_1=27\mathrm{.}96kNm$

Recall the stiffness method formulation for beam elements.

$\{[F_{}],[F_{yi}],[M_i],[F_{xj}],[F_{yj}],[M_j]\}=\left[\begin{array}{cccccc}A\frac{E}{L}& 0& 0& -A\frac{E}{L}& 0& 0\\ 0& 12E\frac{\text{I}}{L^3}& -6E\frac{\text{I}}{L^2}& 0& -12E\frac{\text{I}}{L^3}& -6E\frac{\text{I}}{L^2}\\ 0& -6E\frac{\text{I}}{L^2}& 4E\frac{\text{I}}{L}& 0& 6E\frac{\text{I}}{L^2}& 2E\frac{\text{I}}{L}\\ -A\frac{E}{L}& 0& 0& A\frac{E}{L}& 0& 0\\ 0& -12E\frac{\text{I}}{L^3}& 6E\frac{\text{I}}{L^2}& 0& 12E\frac{\text{I}}{L^3}& 6E\frac{\text{I}}{L^2}\\ 0& -6E\frac{\text{I}}{L^2}& 2E\frac{\text{I}}{L}& 0& 6E\frac{\text{I}}{L^2}& 4E\frac{\text{I}}{L}\end{array}\right]\{[v_i],[v_i],[{}_i],[u_j],[v_j],[{}_j]\}$

Keep in mind that ${}_{ij}$ is the angle between element local $x$ axis and global $x$ axis and that ${}_i$ is the rotation at node $i.$ The complete stiffness method formulation for the frame is: