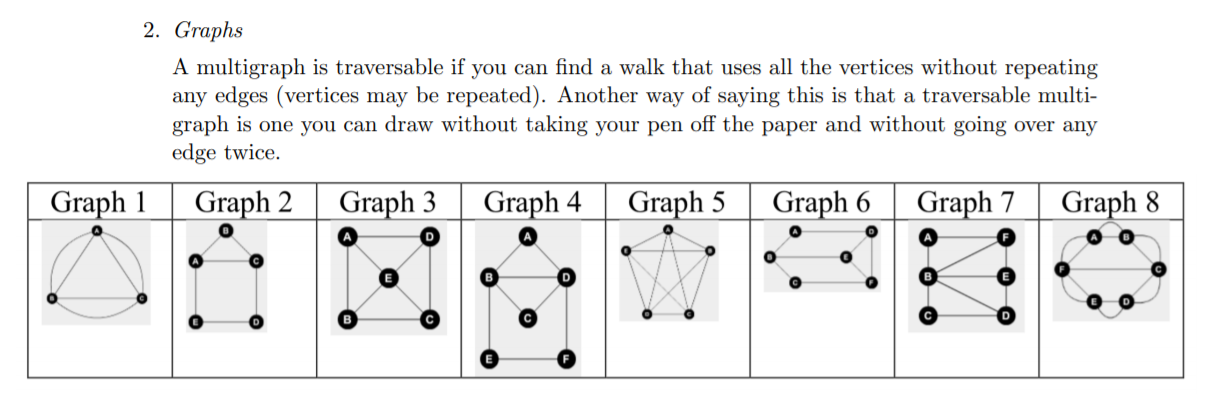
2. Graphs A multigraph is traversable if you can find a walk that uses all the vertices without repeating any edges (vertices may be repeated). Another way of saying this is that a traversable multi- graph is one you can draw without taking your pen off the paper and without going over any edge twice. Graph 1 Graph 2 Graph 3 Graph 4 Graph 5 Graph 6 Graph 7 Graph 8 (a) For each of the given multigraphs, state whether or not it is traversable. (b) With some of the traversable graphs above, you will have found a walk that starts and ends at the same vertex, while for other traversable graphs, your walk will have started and ended at different vertices. Considering, in particular, the degree of each vertex, what common property do you notice that lets you to predict into which of these groups any traversable graph will fit? You must demonstrate clearly how you arrived at this claim! (c) Find a condition that will guarantee a graph is not traversable and provide a convincing argument for why this works