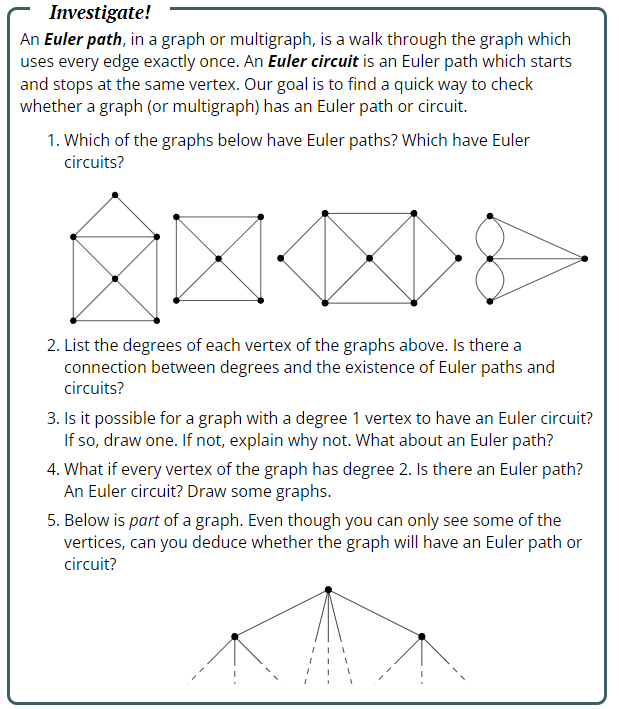
Investigate! An Euler path, in a graph or multigraph, is a walk through the graph which uses every edge exactly once. An Euler circuit is an Euler path which starts and stops at the same vertex. Our goal is to find a quick way to check whether a graph (or multigraph) has an Euler path or circuit, 1. Which of the graphs below have Euler paths? Which have Euler circuits? S8 2. List the degrees of each vertex of the graphs above. Is there a connection between degrees and the existence of Euler paths and circuits? 3. Is it possible for a graph with a degree 1 vertex to have an Euler circuit? If so, draw one. If not, explain why not. What about an Euler path? 4. What if every vertex of the graph has degree 2. Is there an Euler path? An Euler circuit? Draw some graphs. 5. Below is part of a graph. Even though you can only see some of the vertices, can you deduce whether the graph will have an Euler path or circuit? Please help me with these questions on Planar graphs and Euler trails and Euler circuits: (Handwritten please ) Investigate! When a connected graph can be drawn without any edges crossing, it is called planar. When a planar graph is drawn in this way, it divides the plane into regions called faces. 1. Draw, if possible, two different planar graphs with the same number of vertices, edges, and faces. 2. Draw, if possible, two different planar graphs with the same number of vertices and edges, but a different number of faces. Investigate! For the complete graphs K,,, we would like to be able to say something about the number of vertices, edges, and (if the graph is planar) faces. Let's first consider Ka: 1. How many vertices does K5 have? How many edges? 2.If Kais planar, how many faces should it have? Repeat parts (1) and (2) for K4, K5, and K. What about complete bipartite graphs? How many vertices, edges, and faces (if it were planar) does K7 4 have? For which values of m and n are K, and K., . planar? Investigate! A cube is an example of a convex polyhedron. It contains 6 identical squares for its faces, 8 vertices, and 12 edges. The cube is a regular polyhedron (also known as a Platonic solid) because each face is an identical regular polygon and each vertex joins an equal number of faces. There are exactly four other regular polyhedra: the tetrahedron, octahedron, dodecahedron, and icosahedron with 4, 8, 12 and 20 faces respectively. How many vertices and edges do each of these have