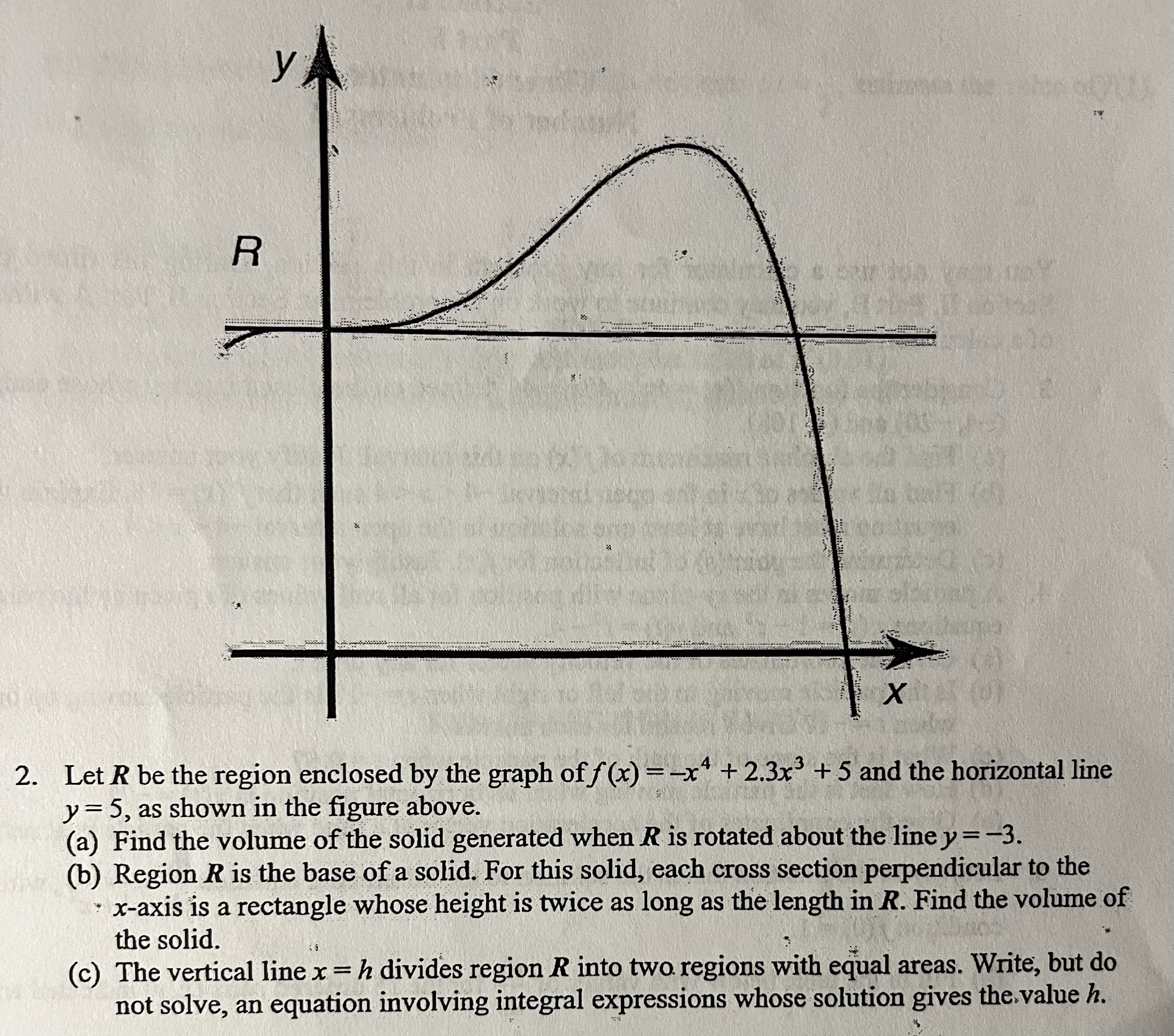
Question: 2 . Let ( R ) be the region enclosed by the graph of ( f ( x ) = - x
Let R be the region enclosed by the graph of fxx x and the horizontal line y as shown in the figure above.
a Find the volume of the solid generated when boldsymbolR is rotated about the line y
b Region boldsymbolR is the base of a solid. For this solid, each cross section perpendicular to the x axis is a rectangle whose height is twice as long as the length in R Find the volume of the solid.
c The vertical line xh divides region R into two regions with equal areas. Write, but do not solve, an equation involving integral expressions whose solution gives the value h
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


