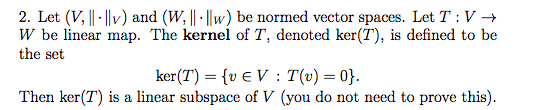
2. Let (V, I. ||v) and ( W W ) be normed vector spaces. Let T:V W be linear map. The kernel of T, denoted ker(T), is defined to be the set ker(T) = {ver not need to prove this). Then ker(T) is a linear subspace of V (you do not need to prove this). (b) Assume that (V. II:llv) is a Banach space. Let T1, T2, T3,... be a sequence of continuous linear maps from (V, II. ||v) to (W, II:llw). Assume that no T, is the constant zero map, i.e., assume that for every i E N there is some v eV with T (0) * 0. Prove that there is some v E V such that for every i E N we have T(v) 70. (10 points) 2. Let (V, I. ||v) and ( W W ) be normed vector spaces. Let T:V W be linear map. The kernel of T, denoted ker(T), is defined to be the set ker(T) = {ver not need to prove this). Then ker(T) is a linear subspace of V (you do not need to prove this). (b) Assume that (V. II:llv) is a Banach space. Let T1, T2, T3,... be a sequence of continuous linear maps from (V, II. ||v) to (W, II:llw). Assume that no T, is the constant zero map, i.e., assume that for every i E N there is some v eV with T (0) * 0. Prove that there is some v E V such that for every i E N we have T(v) 70. (10 points)