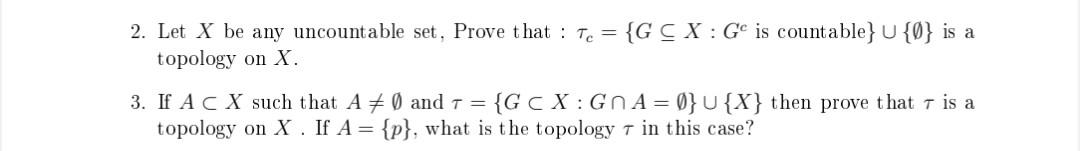
2. Let X be any uncountable set, Prove that : Tc = {G CX:G is countable} U {0} is a topology on X 3. If A C X such that A + ) and 7 = {GCX: GnA=0}U{X} then prove that 7 is a topology on X. If A= {p}, what is the topology t in this case? 2. Let X be any uncountable set, Prove that : Tc = {G CX:G is countable} U {0} is a topology on X 3. If A C X such that A + ) and 7 = {GCX: GnA=0}U{X} then prove that 7 is a topology on X. If A= {p}, what is the topology t in this case