Question: ( 2 points ) Find the limit: ( 2 points ) Find a parametrization of the circle of radius 4 in the x y -
points
Find the limit:
points Find a parametrization of the circle of radius in the plane, centered at the origin, oriented clockwise. The point should correspond to Use as the parameter for all of your answers.
points Find a vector parametric equation vec for the line through the points and for each of the given conditions on the parameter
a If vec:: and vec:: then
vec
b If vec and vec then
vec
c If the points and correspond to the parameter values and respectively, then
vec
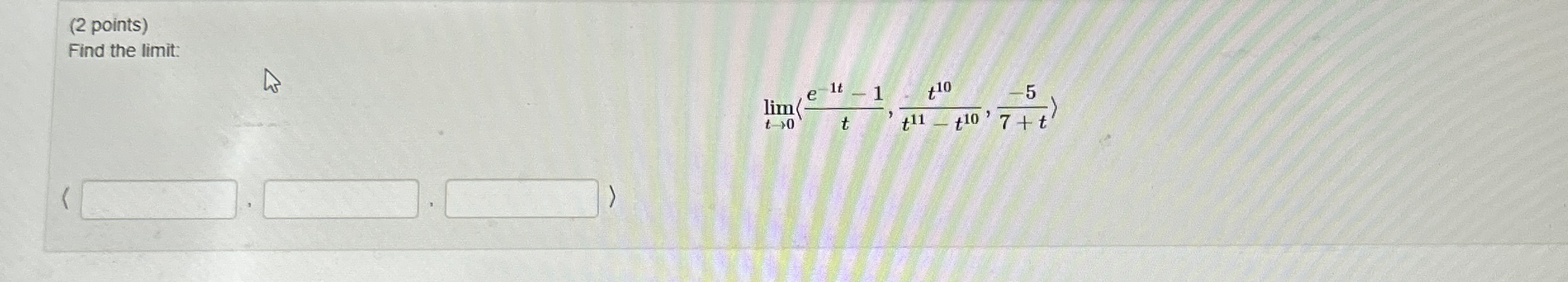
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


