Please help

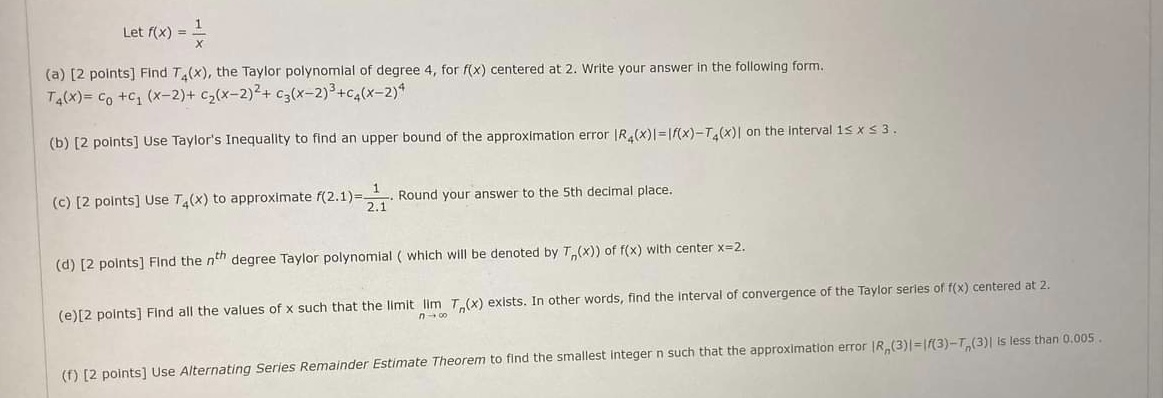
Let f(x) = 1 X (a) [2 points] Find T(x), the Taylor polynomial of degree 4, for f(x) centered at 2. Write your answer in the following form. Ta(x)= Co +61 (x-2)+ C2(x-2)2+ C3(x-2)3+C4(x-2)* (b) [2 points] Use Taylor's Inequality to find an upper bound of the approximation error |R (x) |=[f(x)-T,(x)| on the interval 1s x s 3. (c) [2 points] Use T(x) to approximate f(2.1)=- Round your answer to the 5th decimal place. 2.1 (d) [2 points] Find the n degree Taylor polynomial ( which will be denoted by T,,(x)) of f(x) with center x=2. (e)[2 points] Find all the values of x such that the limit lim T (x) exists. In other words, find the Interval of convergence of the Taylor series of f(x) centered at 2. (f) [2 points] Use Alternating Series Remainder Estimate Theorem to find the smallest integer n such that the approximation error [R,,(3) |=If(3)-T,,(3) | is less than 0.005