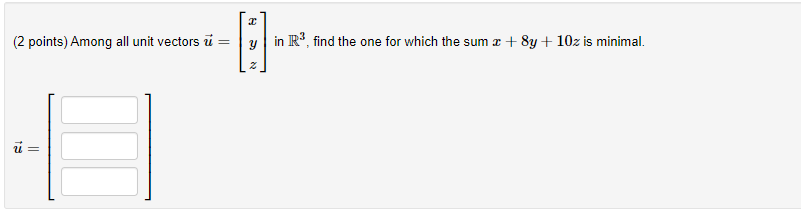
(2 points) You are looking down at a map. A vector u with |u| = 1 points north and a vector v with |v|= 2 points northeast. The crossproduct u x v points: A) south B) northwest C) up D) down Please enter the letter of the correct answer: The magnitude u v| = (2 points) If v (5, 1, -3) and vw = 4, find tan(e), where is the angle between and w. tan(0) = (2 points) Find a unit vector with positive first coordinate that is orthogonal to the plane through the points P = (0, 4, -5), Q = (4, 8, -1), and R = (4, 8, 4). (2 points) Find the shortest distance from the point P = (5,2, -6) to a point on the line given by 1: (x, y, z) = (-6t, 5t, 5t). The distance is x (2 points) Among all unit vectors u = y in R, find the one for which the sum x + 8y + 10z is minimal. 2 13 =