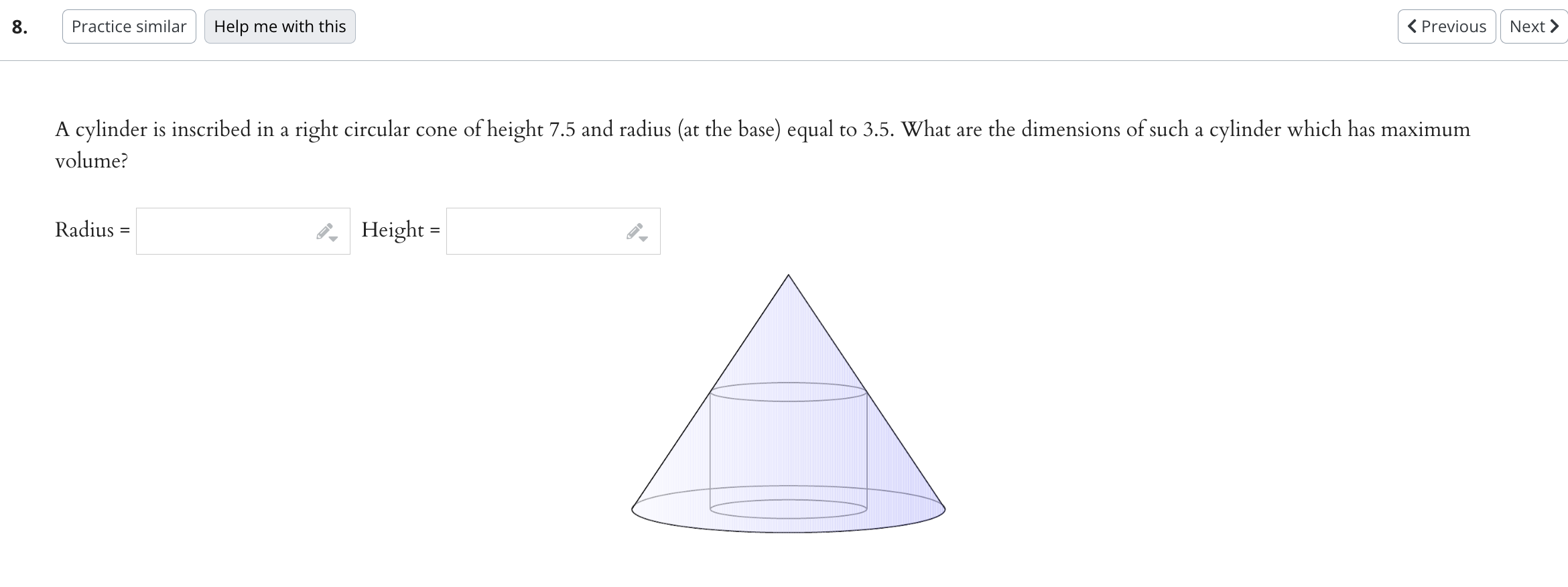
2. Practice similar Help me with this l ( Previous Next ) A printed poster is to have a total area of 671 square inches with top and bottom margins of 3 inches and side margins of 2 inches. What should be the dimensions of the poster so that the printed area be as large as possible? (Round your answers to three decimal places if necessary, but do not round until your nal computation.) a. To solve, let an denote the width of the poster in inches and let y denote the length in inches. We need to maximize the following function ofa: and y. Area in terms of a: and y: b. We can reexpress this as the following function ofm alone. f($) : c. We nd that f(x) has a critical zvalue, denoted m5. mg 2 d. To verify that at) has a maximum at this critical number we compute the second derivative f\"(:c) and nd that its value at the critical number. f(Ec) = is a P v number e. We determine the optimal dimensions of the poster. :3 = inches by y = inches f. Finally, this gives us a maximumal printed area. Area: square inches 3. Practice similar Help me with this