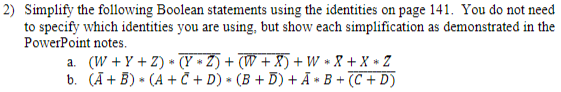
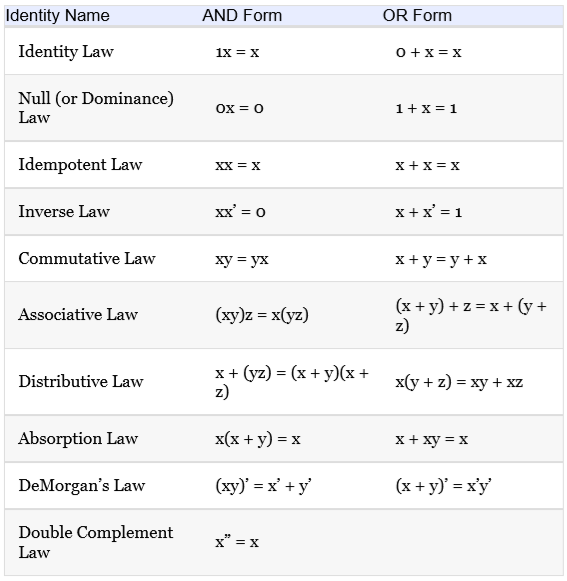
2) Simplify the following Boolean statements using the identities on page 141. You do not need to specify which identities you are using, but show each simplification as demonstrated in the PowerPoint notes. a. (W+Y+Z) (Y Z) + (W + 8) +W*X+X*Z K b. (A + B) (A + C + D) (B + D) + A + B + (C+D) * Identity Name Identity Law Null (or Dominance) Law Idempotent Law Inverse Law Commutative Law Associative Law Distributive Law Absorption Law DeMorgan's Law Double Complement Law AND Form 1X = X OX = 0 XX = X XX' = 0 xy = yx (xy)z = x(yz) x + (yz) = (x+y)(x + z) x(x + y) = x (xy)' = x + y X" = = X OR Form 0 +X = X 1 + x = 1 X+X=X X+X' = 1 x+y = y + x (x + y) + z = x + (y + z) x(y + z) = xy + xz x + xy = x (x+y)' = x'y