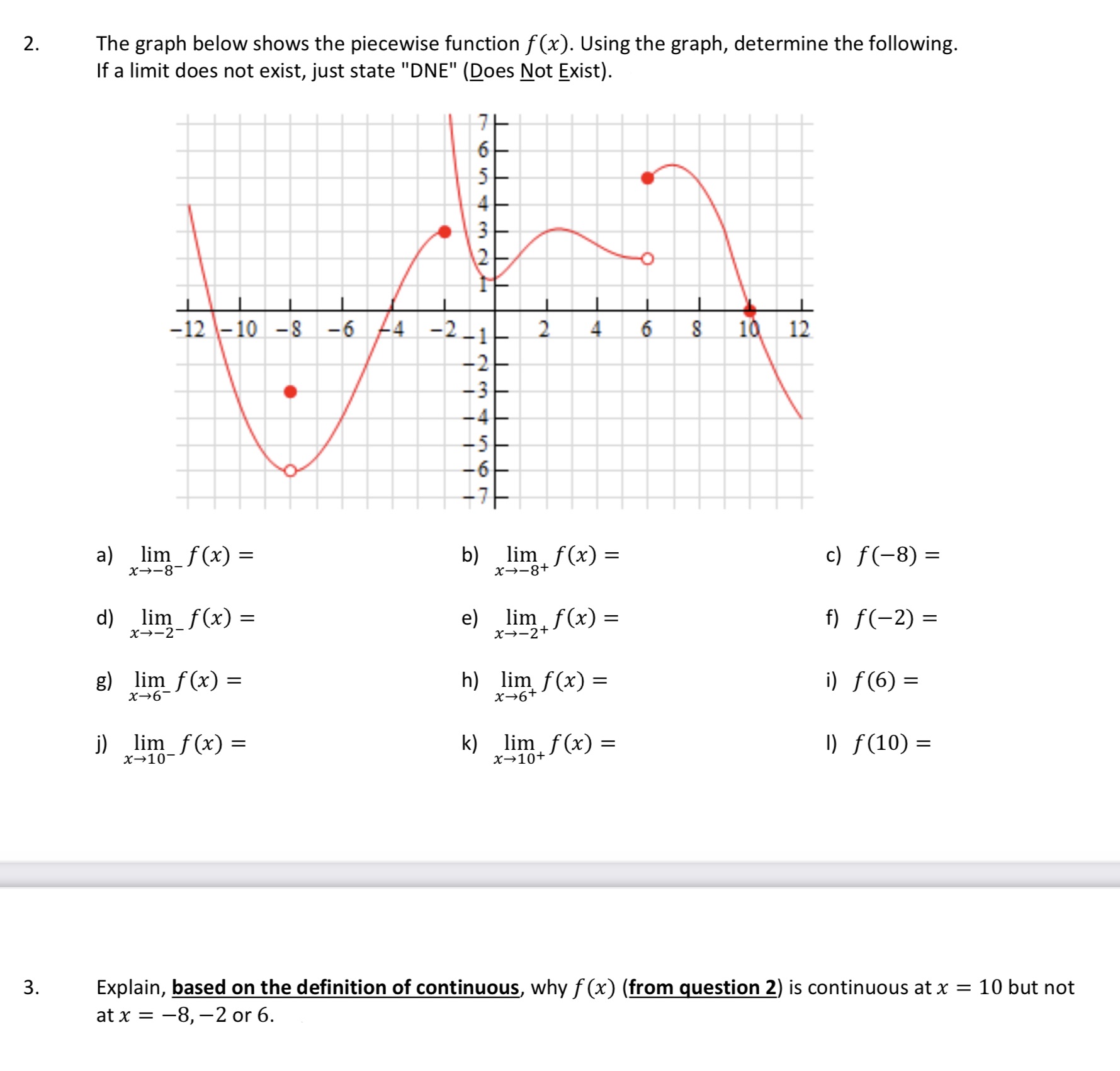
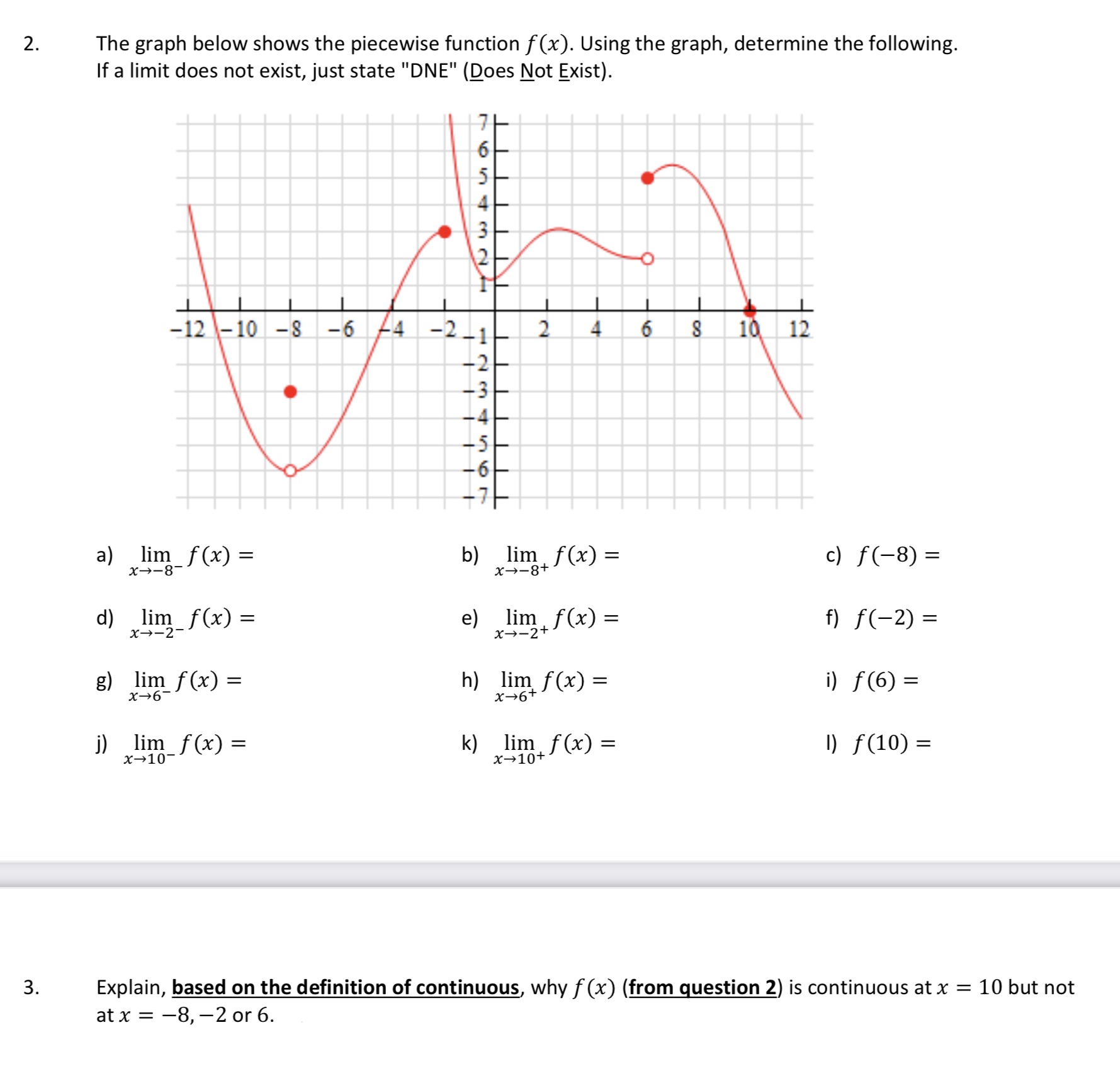
2. The graph below shows the piecewise function f (x). Using the graph, determine the following If a limit does not exist, just state "DNE" (Does Not Exist). -12 -10 -8 -6 4 -2 -1 2 4 $ 10 12 a) lim f (x) = b) lim f (x) = X - -8- X - - 8+ c) f ( -8) = d) lim f(x) = X - - 2 - e) lim f(x) = X - - 2+ f ) f ( - 2 ) = g) lim f (x) = h) lim f(x) = X -+6- i) f (6) = x-6+ j) lim_f (x) = k) lim f (x) = x-10 x-10+ 1) f (10) = 3. Explain, based on the definition of continuous, why f (x) (from question 2) is continuous at x = 10 but not at x = -8, -2 or 6