please solve the questions in the pictures!

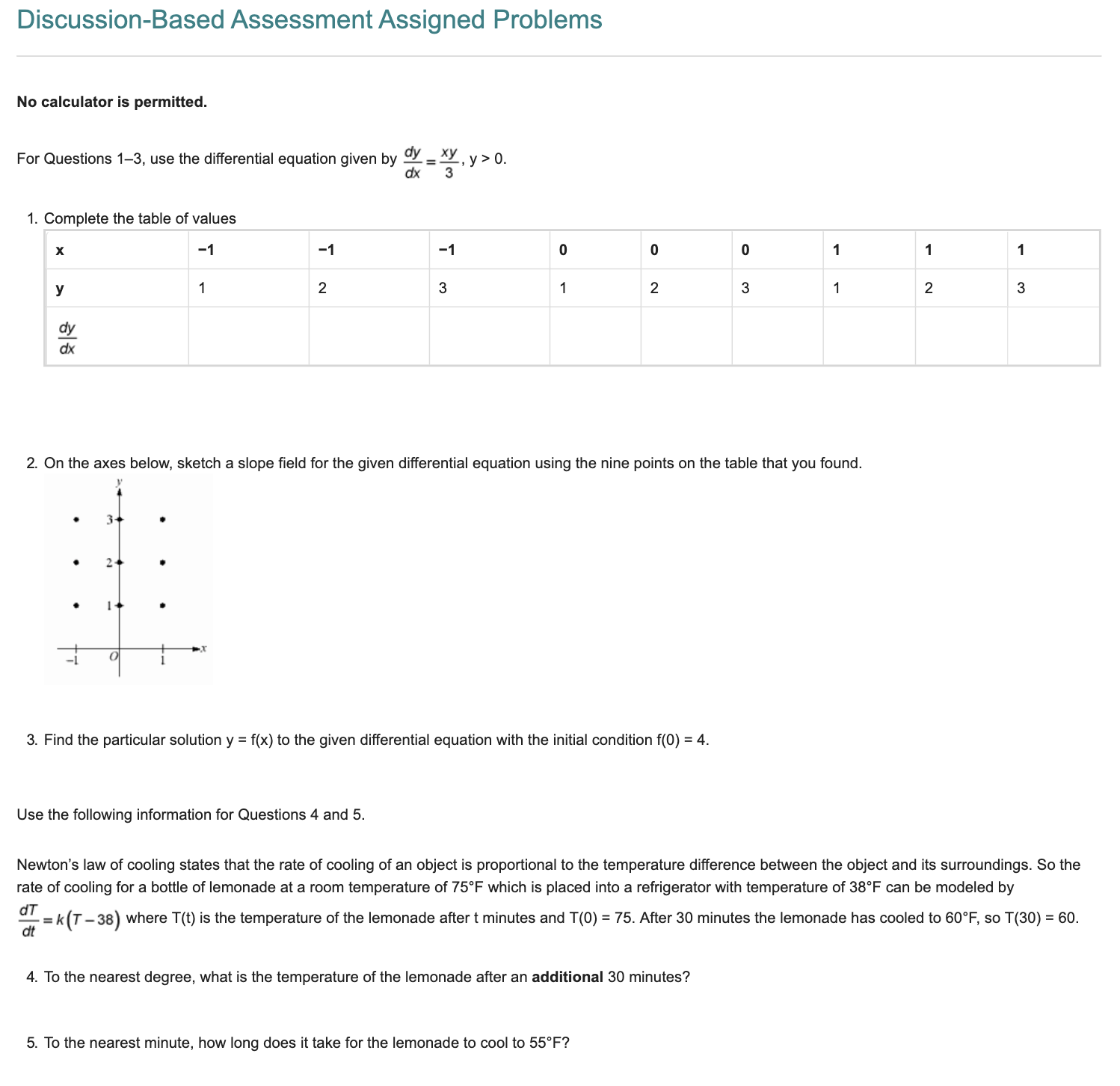
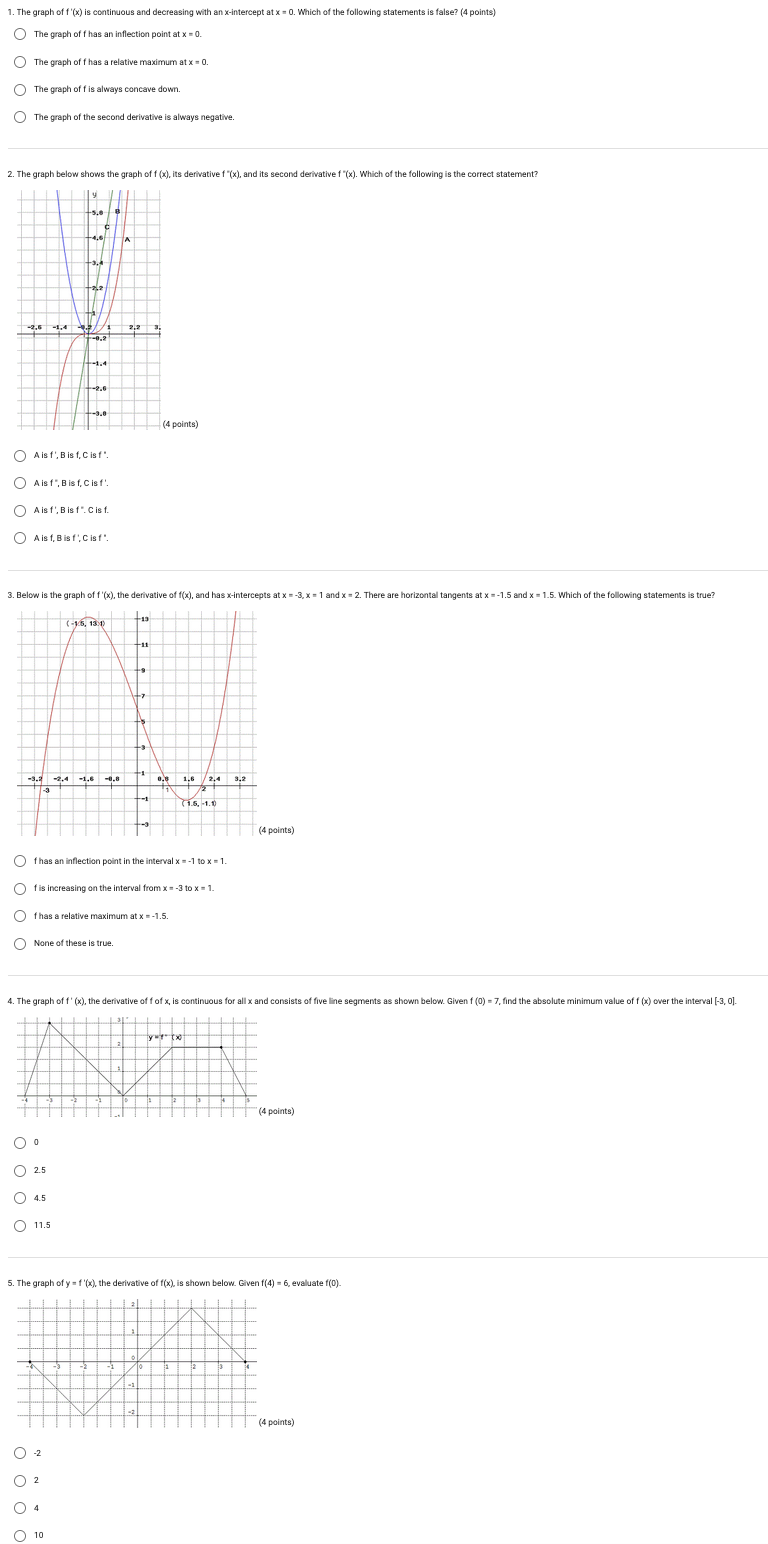
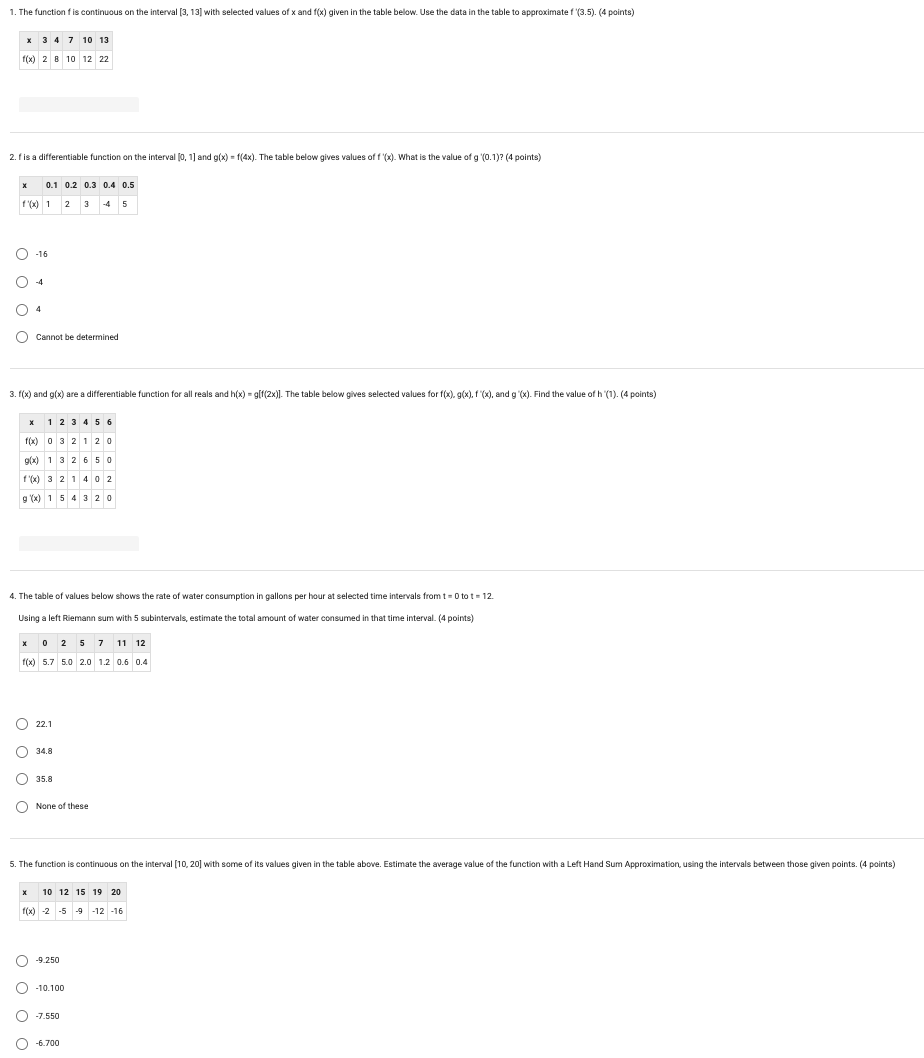
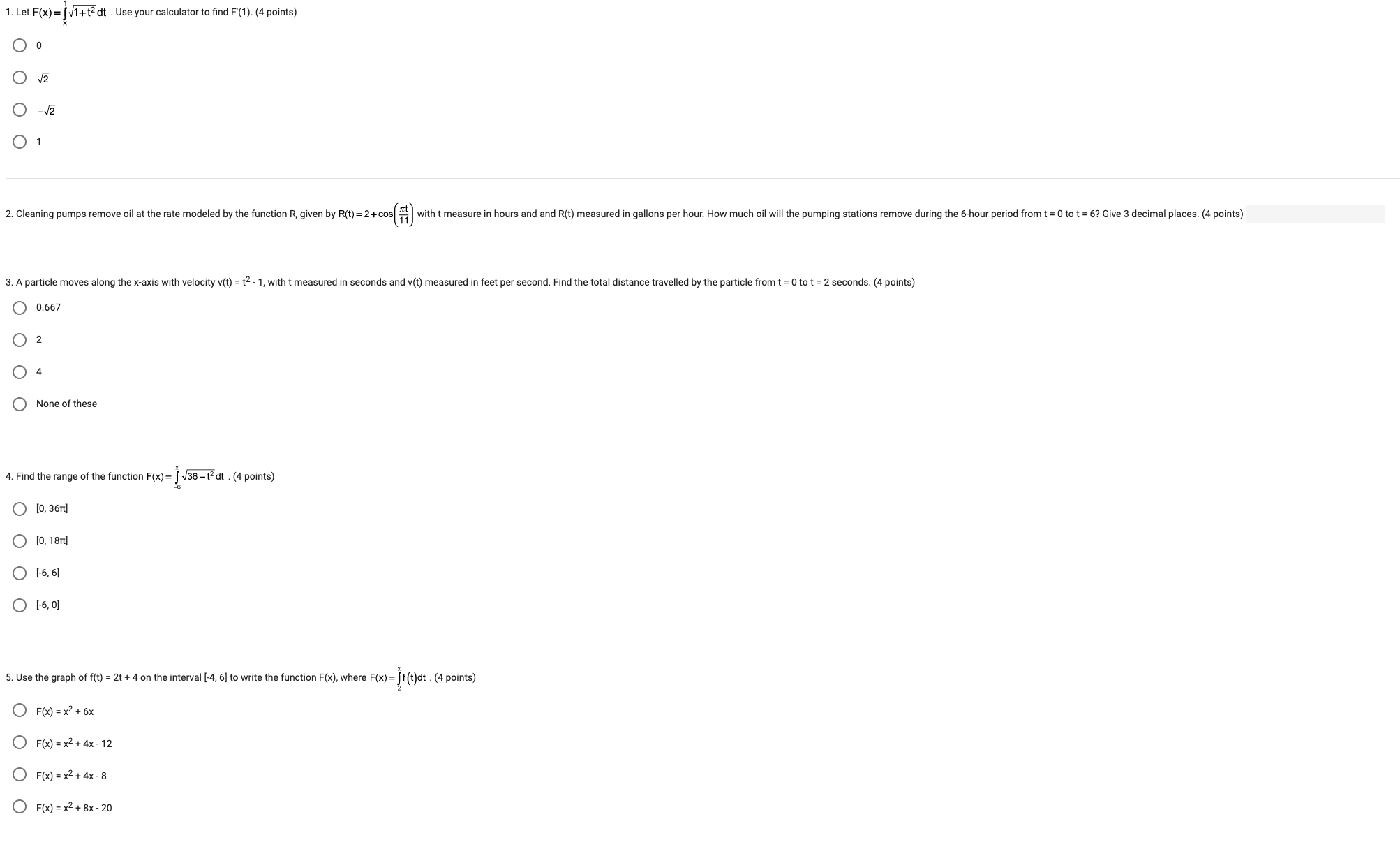
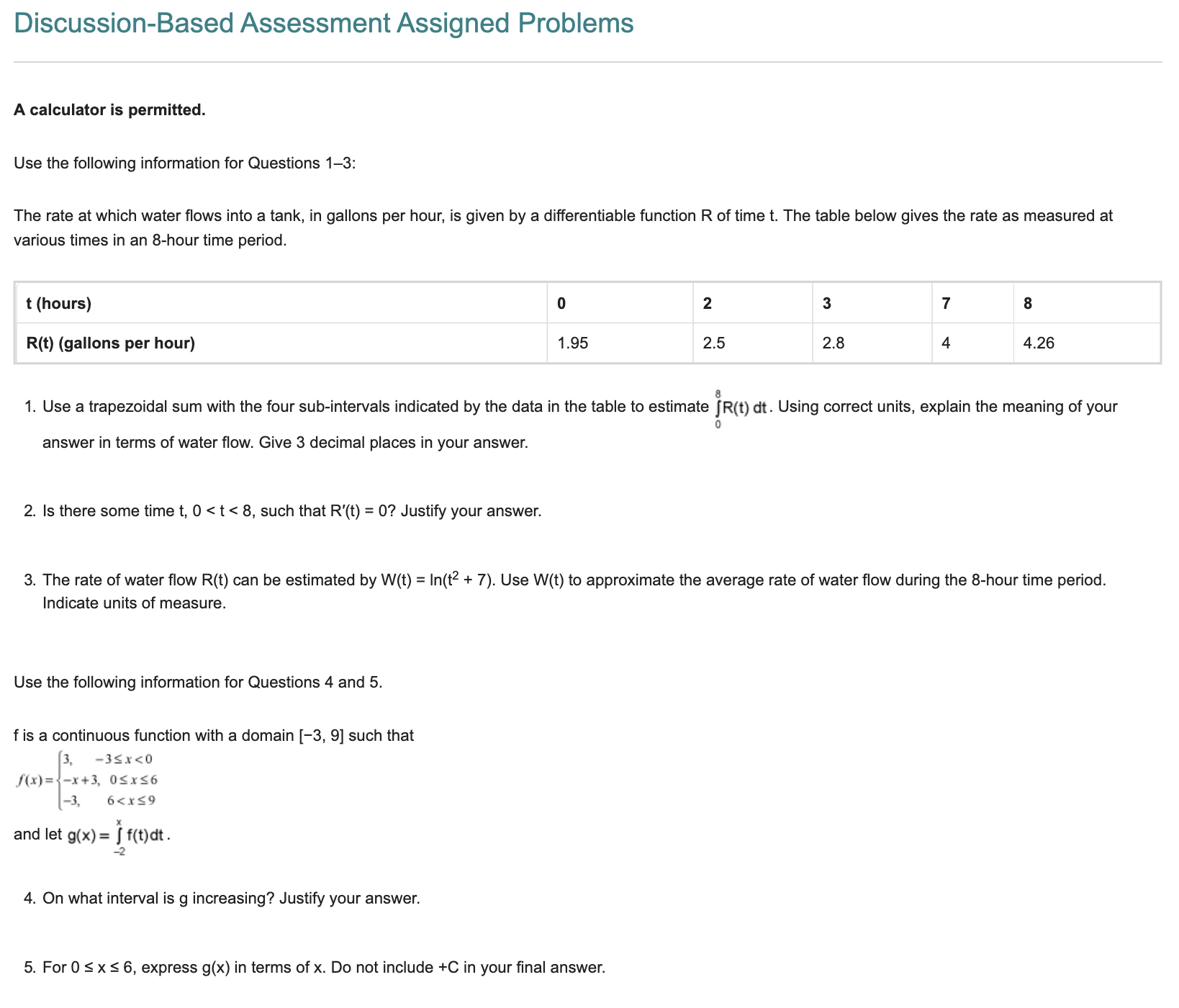
1 1. Which of the following values would be obtained using 10 circumscribed rectangles of equal width (an upper sum) to estimate gxzdx 7 (4 points) O oars (@KL O 1380 O 2310 b, 2. Which definite integral approximation formula is | f(x)dx ;b'Ta[yyya +.. +y,__|+y,'} 7 (4 points) 2 O Leftrectangles O Right rectangles (O Average rate of change (O Trapezoidal rule 2 3. The estimated value of !xzdx , using the trapezoidal rule with 4 trapezoids is (4 points) QO 275 O ss0 O 188 O 375 4. Given the table below for selected values of f(x), use 6 right rectangles to estimate the value of 10 [ f(x)ax q . (4 points) x 1346 7 9 10 f(x) 4 8 6 10 10 12 16 b 5. Function f(x) is positive, decreasing and concave up on the closed interval [a, b]. The interval [a, b] is partitioned into 4 equal intervals and these are used to compute the left sum, right sum, and trapezoidal rule approximations for the value of | f(x]dx Which one of the following statements is true? (4 points) a (O Leftsum 0. 1. Complete the table of values X -1 -1 -1 0 0 0 1 1 1 y 1 2 3 1 2 3 1 2 3 dx 2. On the axes below, sketch a slope field for the given differential equation using the nine points on the table that you found. y 3. Find the particular solution y = f(x) to the given differential equation with the initial condition f(0) = 4. Use the following information for Questions 4 and 5. Newton''s law of cooling states that the rate of cooling of an object is proportional to the temperature difference between the object and its surroundings. So the rate of cooling for a bottle of lemonade at a room temperature of 75F which is placed into a refrigerator with temperature of 38F can be modeled by dT " k (T _33) where T(t) is the temperature of the lemonade after t minutes and T(0) = 75. After 30 minutes the lemonade has cooled to 60F, so T(30) = 60. 4. To the nearest degree, what is the temperature of the lemonade after an additional 30 minutes? 5. To the nearest minute, how long does it take for the lemonade to cool to 55F? 1. The graph of f'(x) is continuous and decreasing with an x-intercept at x = 0. Which of the following statements is false? (4 points) The graph of f has an inflection point at x = 0. The graph of f has a relative maximum at x = 0. The graph of f is always concave down. The graph of the second derivative is always negative. 2. The graph below shows the graph of f (x), its derivative f "(x), and its second derivative f "(x). Which of the following is the correct statement? -2.5 -1.4 2.2 (4 points) ( Aist', Bist, Cist". ( Aist', Bist, Cist! Aist ', Bist". Cist. ) Aist, Bist '; Cist". 3. Below is the graph of f'(x), the derivative of f(x), and has x-intercepts at x = -3, x = 1 and x = 2. There are horizontal tangents at x =-1.5 and x = 1.5. Which of the following statements is true? -3.2 -2.4 -1.6 -0.8 0.3 1.6 2.4 3.2 71.5. 1.0 (4 points) Of has an inflection point in the interval x = -1 to x = 1. Of is increasing on the interval from x = -3 to x = 1. f has a relative maximum at x = -1.5. None of these is true. 4. The graph of f' (x), the derivative of f of x, is continuous for all x and consists of five line segments as shown below. Given f (0) = 7, find the absolute minimum value of f (x) over the interval [-3, 0]. (4 points) O . O 2.5 O 4.5 11.5 5. The graph of y = f'(x), the derivative of f(x), is shown below. Given f(4) = 6, evaluate f(0). (4 points) 101. Which of the following functions grows the fastest as x goes to infinity? (4 points) O = O Ink O sin(x) x20 2. Compare the rates of growth of f(x) = e*5* and g(x) = e* as x approaches infinity. (4 points) O f(x) grows faster than g(x) as x goes to infinity. O g(x) grows faster than f(x) as x goes to infinity. O f(x) and g(x) grow at the same rate as x goes to infinity. (O) The rate of growth cannot be determined. 3. What does |im T =() show? (4 points) x==g(X) O g(x) grows faster than f(x) as x goes to infinity. O f(x) and g(x) grow at the same rate as x goes to infinity. O f(x) grows faster than g(x) as x goes to infinity. 'Hapital's Rule must be used to determine the true limit value. 4. Which of the following functions grows at the same rate as e* as x goes to infinity? (4 points) O ews O o O e O e 5. Which of the following functions grows the slowest as x goes to infinity? (4 points) O x O & O ex (O Theyall grow at the same rate. 1. The function f is continuous on the interval [3, 13] with selected values of x and f(x) given in the table below. Use the data in the table to approximate f '(3.5). (4 points) x 3 4 7 10 13 1(x) 2 8 10 12 22 2. f is a differentiable function on the interval [0, 1] and g(x) = f(4x). The table below gives values of f \\(x). What is the value of g '(0.1)? (4 points) 0.1 0.2 0.3 0.4 0.5 1 1x) 1 2 3 -4 5 O -16 0 4 O 4 O Cannot be determined 3. f(x) and g(x) are a differentiable function for all reals and h(x) = g[f(2x)]. The table below gives selected values for f(x). g(x), f (x), and g"(x). Find the value of h "(1). (4 points) 1 2 3 4 5 6 1(x) 0 3 2 1 2 0 g(x) 1 3 2 6 5 0 1 1 x) 3 2 1 4 0 2 g (x) 1 5 4 3 2 0 4. The table of values below shows the rate of water consumption in gallons per hour at selected time intervals from t = 0 to t = 12. Using a left Riemann sum with 5 subintervals, estimate the total amount of water consumed in that time interval. (4 points) 0 2 5 7 11 12 1(x) 5.7 5.0 2.0 1.2 0.6 0.4 22.1 34.8 35.8 None of these 5. The function is continuous on the interval [10, 20] with some of its values given in the table above. Estimate the average value of the function with a Left Hand Sum Approximation, using the intervals between those given points. (4 points) * 10 12 15 19 20 1(x) -2 -5 -9 -12 -16 -9.250 -10.100 -7.550 -6.7001. Let F(x)=[ V1+12 dt . Use your calculator to find F'(1). (4 points) O . O VZ O -V2 O 1 2. Cleaning pumps remove oil at the rate modeled by the function R, given by R(t) = 2+ cos| |with t measure in hours and and R(t) measured in gallons per hour. How much oil will the pumping stations remove during the 6-hour period from t = 0 to t = 6? Give 3 decimal places. (4 points) 3. A particle moves along the x-axis with velocity v(t) = t2 - 1, with t measured in seconds and v(t) measured in feet per second. Find the total distance travelled by the particle from t = 0 to t = 2 seconds. (4 points) 0.667 O 2 0 4 None of these 4. Find the range of the function F(x) = ] V36 -12 at . (4 points) O [0, 3671] O [0, 18rt] O [-6, 6] O [-6, 0] 5. Use the graph of f(t) = 2t + 4 on the interval [-4, 6] to write the function F(x), where F(x) = ff(t)at . (4 points) OF(x) = x2 +6x O F(x) = x2 +4x - 12 OF(x) =x2 +4x - 8 OF(x) = x2 + 8x - 20Discussion-Based Assessment Assigned Problems A calculator is permitted. Use the following information for Questions 1-3: The rate at which water flows into a tank, in gallons per hour, is given by a differentiable function R of time t. The table below gives the rate as measured at various times in an 8-hour time period. t (hours) 0 2 3 7 8 R(t) (gallons per hour) 1.95 25 28 4 4.26 8 1. Use a trapezoidal sum with the four sub-intervals indicated by the data in the table to estimate [R(t) dt. Using correct units, explain the meaning of your 0 answer in terms of water flow. Give 3 decimal places in your answer. 2. Is there some time t, 0