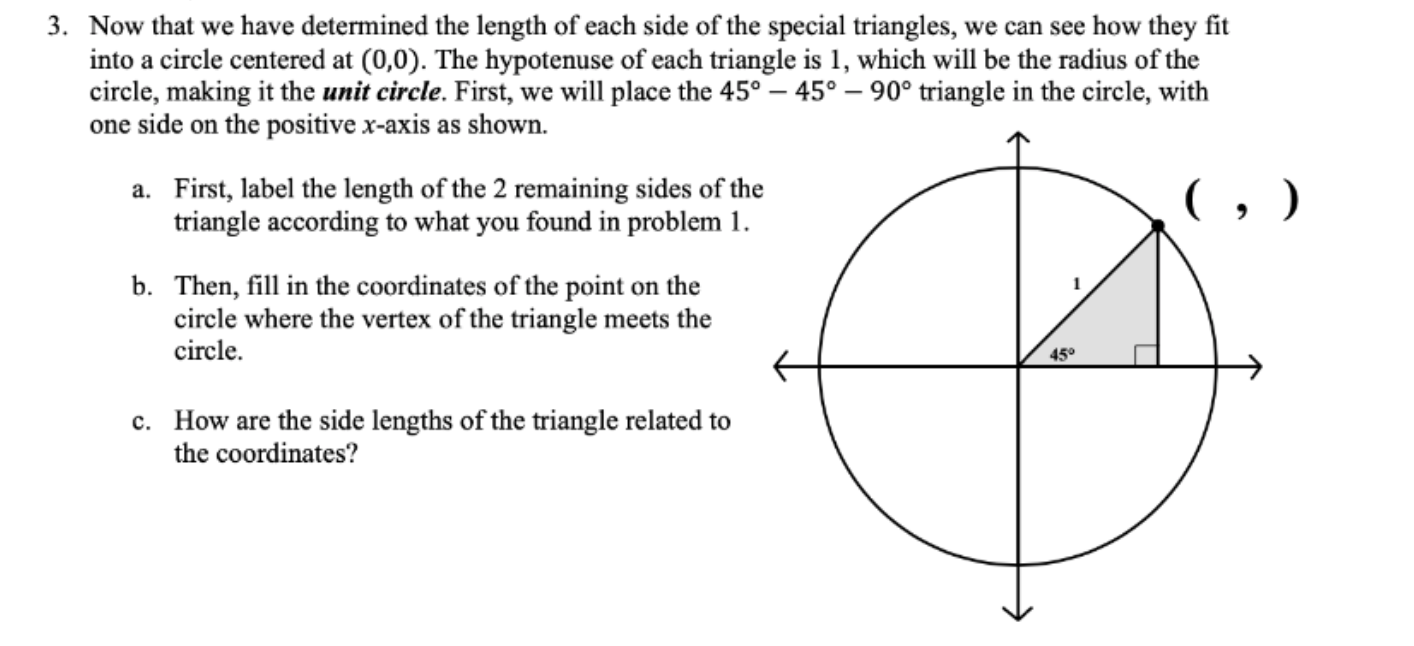
2. The second special triangle is the 30 - 60-90 triangle. We can see the special properties of this triangle by constructing the triangle starting with an equilateral triangle of side length 1. a. What is the measure of each of the angles of the equilateral triangle? How do you know? b. Drawing in an altitude of the equilateral triangle bisects the angle at the top of the triangle. i. What is the measure of the new angle, 0? ii. What is the measure of y? c. Now, take one of the smaller triangles. What is the measure of z? Use that handy theorem again, and remember to state the EXACT answer, no decimals. A 3. Now that we have determined the length of each side of the special triangles, we can see how they fit into a circle centered at (0,0). The hypotenuse of each triangle is 1, which will be the radius of the circle, making it the unit circle. First, we will place the 45-45-90 triangle in the circle, with one side on the positive x-axis as shown. a. First, label the length of the 2 remaining sides of the triangle according to what you found in problem 1. b. Then, fill in the coordinates of the point on the circle where the vertex of the triangle meets the circle. c. How are the side lengths of the triangle related to the coordinates? 45 , )