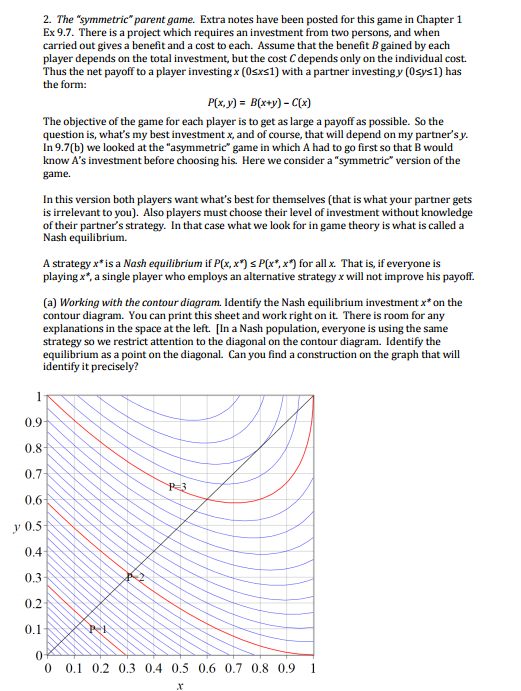
2. The "symmetric" parent game. Extra notes have been posted for this game in Chapter 1 Ex 9.7. There is a project which requires an investment from two persons, and when carried out gives a benefit and a cost to each. Assume that the benefit B gained by each player depends on the total investment, but the cost C depends only on the individual cost. Thus the net payoff to a player investing x (0sxs1) with a partner investing y (0sys1) has the form: P(x,y) B(xy)-C(x) The objective of the game for each player is to get as large a payoff as possible. So the question is, what's my best investment x, and of course, that will depend on my partner'sy. In 9.7(b) we looked at the "asymmetric" game in which A had to go first so that B would know A's investment before choosing his. Here we consider a "symmetric" version of the game In this version both players want what's best for themselves (that is what your partner gets is irrelevant to you). Also players must choose their level of investment without knowledge of their partner's strategy. In that case what we look for in game theory is what is called a Nash equilibrium. A strategy x*is a Nash equilibrium if P(x, xs P[x,x for all x. That is, if everyone is playing x*, a single player who employs an alternative strategy x will not improve his payoff. (a) Working with the contour diagram. Identify the Nash equilibriurn investment x"on the contour diagram. You can print this sheet and work right on it. There is room for any explanations in the space at the left.In a Nash population, everyone is using the same strategy so we restrict attention to the diagonal on the contour diagram. Identify the equilibrium as a point on the diagonal. Can you find a construction on the graph that will identify it precisely? 0.9 0.8 0.7 0.6 y0.5 0.4 0.3 0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 2. The "symmetric" parent game. Extra notes have been posted for this game in Chapter 1 Ex 9.7. There is a project which requires an investment from two persons, and when carried out gives a benefit and a cost to each. Assume that the benefit B gained by each player depends on the total investment, but the cost C depends only on the individual cost. Thus the net payoff to a player investing x (0sxs1) with a partner investing y (0sys1) has the form: P(x,y) B(xy)-C(x) The objective of the game for each player is to get as large a payoff as possible. So the question is, what's my best investment x, and of course, that will depend on my partner'sy. In 9.7(b) we looked at the "asymmetric" game in which A had to go first so that B would know A's investment before choosing his. Here we consider a "symmetric" version of the game In this version both players want what's best for themselves (that is what your partner gets is irrelevant to you). Also players must choose their level of investment without knowledge of their partner's strategy. In that case what we look for in game theory is what is called a Nash equilibrium. A strategy x*is a Nash equilibrium if P(x, xs P[x,x for all x. That is, if everyone is playing x*, a single player who employs an alternative strategy x will not improve his payoff. (a) Working with the contour diagram. Identify the Nash equilibriurn investment x"on the contour diagram. You can print this sheet and work right on it. There is room for any explanations in the space at the left.In a Nash population, everyone is using the same strategy so we restrict attention to the diagonal on the contour diagram. Identify the equilibrium as a point on the diagonal. Can you find a construction on the graph that will identify it precisely? 0.9 0.8 0.7 0.6 y0.5 0.4 0.3 0.2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1