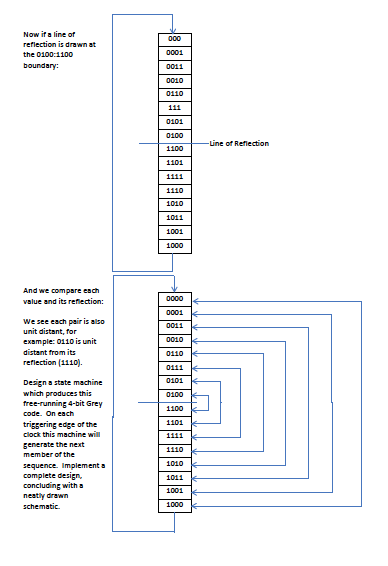
2) We know that a unit distance code is a binary sequence in which each successive value differs from its predecessor by a change in exactly one bit. This is the property that makes K-Maps work. A Grey code is a unit distance code which is reflexive. Consider the following sequence: 000 0001 0011 0010 0110 111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 A close examination will reveal this to be a circular, 4-bit, unit distance code. Now if a line of reflection is drawn at the 0100:1100 boundary: And we compare each value and its reflection: We see each pair is also unit distant, for example: 0110 is unit distant from its reflection (1110). Design a state machine which produces this free-running 4-bit Grey code. On each triggering edge of the clock this machine will generate the next member of the sequence. Implement a complete design, concluding with a neatly drawn schematic 000 0001 0011 0010 0110 111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 -Line of Reflection