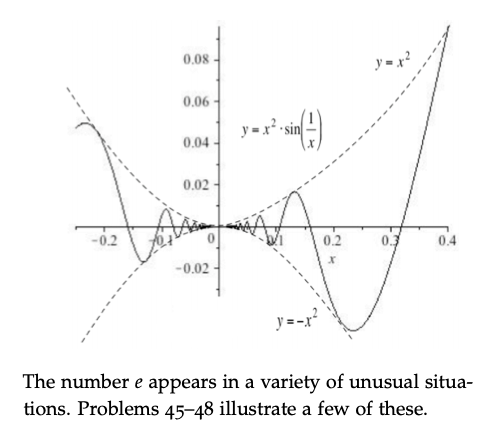
2.2.44 please explain how to get the solution step by step.

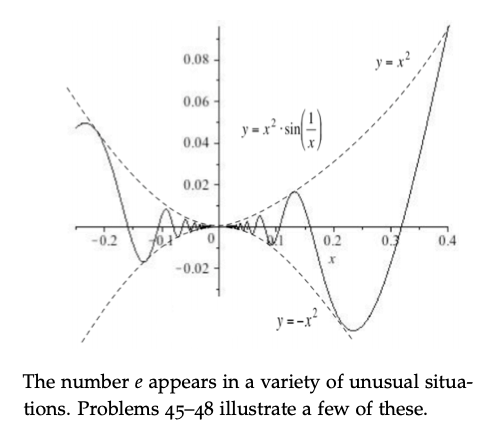
44. The function f(x) defined as f (x ) = x2 . sin(-) if x * 0 0 if x = 0 (shown at the top of the next page) is continuous at 0 because we can show (using the Squeezing Theorem) that lim f(x) = 0 = f(0) h-0 Is f differentiable at 0? To answer this question, use the definition of f' (0) and consider lim f(0 + h) - f(0) h-0 h0.08 0.06 y = x .sin HI- 0.04 0.02 -0.2 0.2 03 0.4 r -0.02 The number e appears in a variety of unusual situa- tions. Problems 45-48 illustrate a few of these