2.4.1 : Proving statements about odd and even integers with direct proofs.

Each statement below involves odd and even integers. An odd integer is an integer that can be expressed as 2k + 1 , where k is an integer. An even integer is an integer that can be expressed as 2k , where k is an integer.

Prove each of the following statements using a direct proof.

(a)

The sum of an odd and an even integer is odd.

(c)

The square of an odd integer is an odd integer.

(e)

If x is an even integer and y is an odd integer, then x^2 + y^2 is odd.

(h)

The negative of an odd integer is also odd.

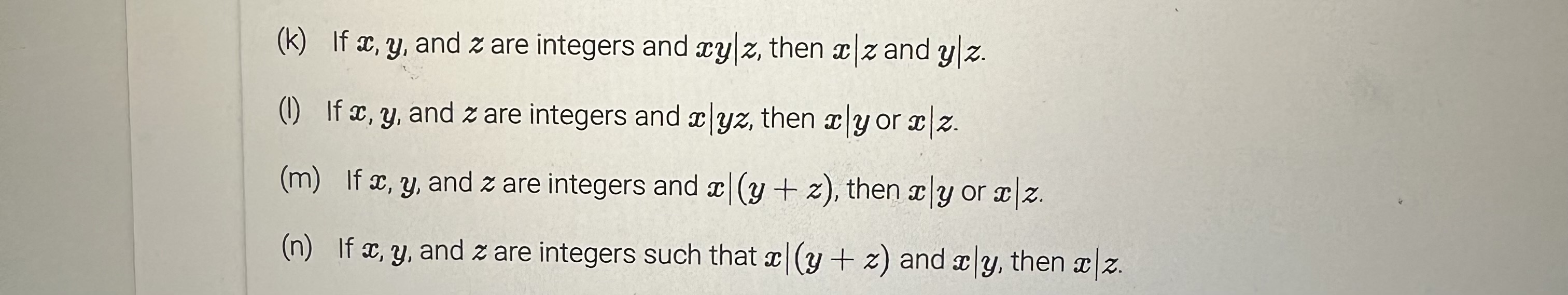
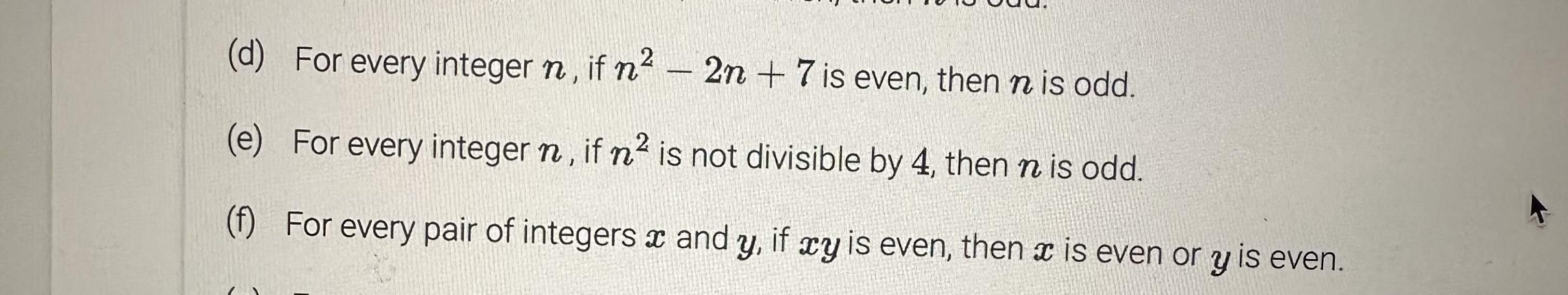
EXERCISE 2.4.2: Proving statements about rational numbers with direct proofs. Prove each of the following statements using a direct proof. (a) The product of two rational numbers is a rational number. (b) The quotient of a rational number and a non-zero rational number is a rational number. (c) If a and y are rational numbers then 3x + 2y is also a rational number. (d) If a and y are rational numbers then 3x2 + 2y is also a rational number. (e) If a and y are rational numbers, where y * 0 and y * -1, then is also rational. 1+ 1 y (f) The average of two rational numbers is also rational.(c) If a2 = y2, then x = y (d) If ac and y are real numbers and a > 1, and x divides y, then x } (y + 1)