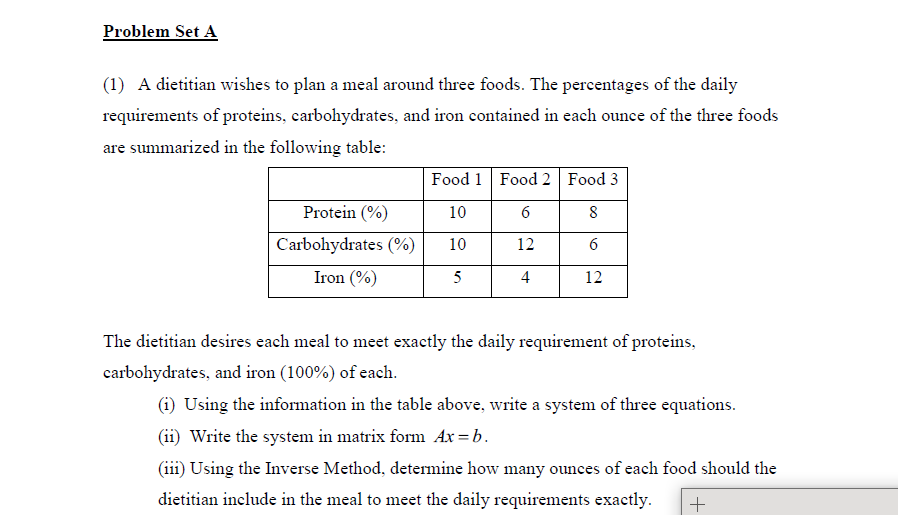
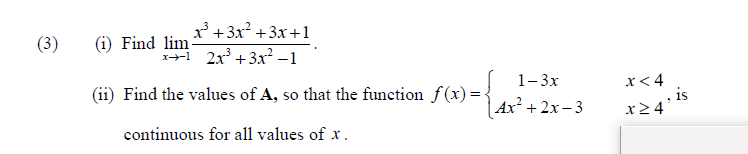
27 (2) For the function f(x) = x+39 3 4 2 (1) Determine the coordinates of the turning points. (ii) Determine the coordinates for the point of inflection if it does exist. (iii) What is the range of value over which the function is decreasing? (iv) What is the range of values over which the function is strictly concave downwards? (3) An instructor wants to create a test that has true-false questions, multiple-choice questions, and essay questions. He wants the test to have 35 questions, with twice as many multiple-choice questions as essay questions and with twice as many true-false questions as multiple-choice questions. (i). Write a system of equations to represent this problem. (11). Hence or otherwise, determine how many of each type of question should the instructor put on the test?Problem Set A (1) A dietitian wishes to plan a meal around three foods. The percentages of the daily requirements of proteins. carbohydrates, and iron contained in each ounce of the three foods are summarized in the following table: Food 1 Food 2 Food 3 Protein ('34:) 10 6 8 Carl) ohydrate s (\"l/o) Iron (94:) 5 4 12 The dietitian desires each meal to meet exactly the daily requirement of proteins. carbohydrates= and iron (100%) of each. (i) Using the information in the table above: write a system of three equations. (ii) Write the system in matrix form Ar = .5. (iii) Using the Inverse Method, determine how many ounces of each food should the dietitian include in the meal to meet the daily requirements exactly. ' + (3) (i) Find lim x' +3x-+3x+1 2x +3x- -1 1-3x x4 (ii) Find the values of A, so that the function f (x) = Ax- +2x-3 , 1S x24' continuous for all values of x.Problem Set B 2 (IJFind 5mm. 1\"?121x3 {2] A stud},r indicates that spending moneyr on pollution control is effective up to a point but eventuallj,F becomes wastell. Suppose it is known that when X million dollars is spent on 100$: controlling pollution' the percentage of pollution removed is given by P(x} = 2 0.03;: +9 {i} At what rate is the percentage of pollution removal P{x) changing when 16 million dollars is spent? Is the percentage increasing or decreasing at this level of expenditure? (ii) For what values of K is HI) increasing? + (iii) For what values of K is HI) decreasing? Take a note... Problem Set C (1) (3) For demand function Q91: :1 bP and supply function Q: = dP c , using Cramer's rule determine equilibrium price and equilibrium quantity. In calm waters, the oil spilling from the ruptured hull of a grounded tanker spreads in all directions. Assuming that the area polluted is a circle and that its radius is increasing at a rate of 2 ftfsec, determine how fast the area is increasing when the radius of the circle is 40 ft. A rms production function is Q(L) = 151.2 {1.1L3 , where output {Q} is a function of a single input labour (L). (i) Find the number of workers required to maximize total product. (ii) For what number of workers is average product maximum