Question: 2B Trigometric Functions ***PLEASE SHOW ALL WORK**** I For Exercises 19, draw the angle using a ray through the origin, and determine whether the sine,
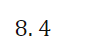
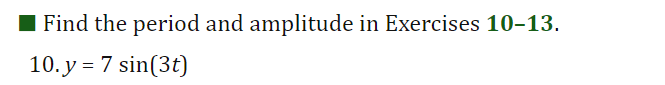
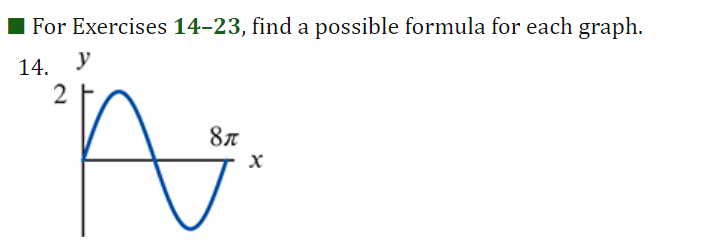

![trigonometric functions on a calculator You are given that sin(7I/12] : 0.259](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667b1a934b8c6_763667b1a93357a0.jpg)
![and cos [11/5] : 0.809. You may want to draw a picture](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667b1a93ba62c_763667b1a93a043a.jpg)
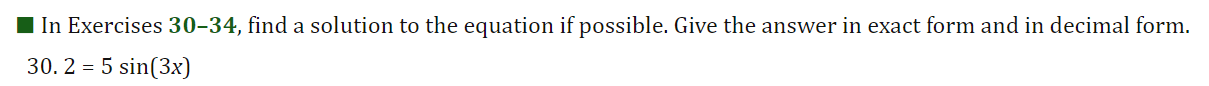
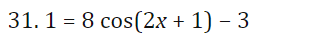
![5 sin(3X] \f41. Without a calculator or computer, match the formulas with](https://s3.amazonaws.com/si.experts.images/answers/2024/06/667b1a9595dd1_765667b1a956d49f.jpg)

2B Trigometric Functions
***PLEASE SHOW ALL WORK****
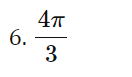
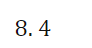
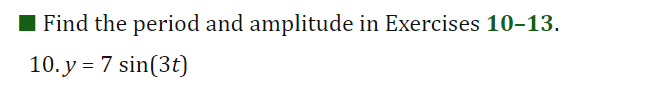
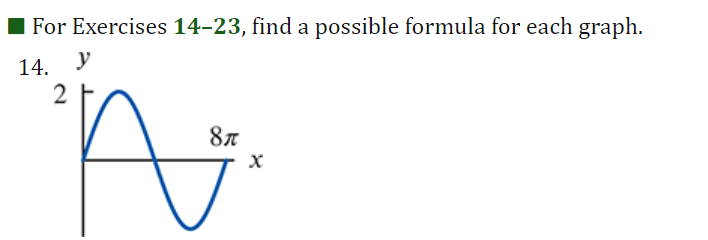
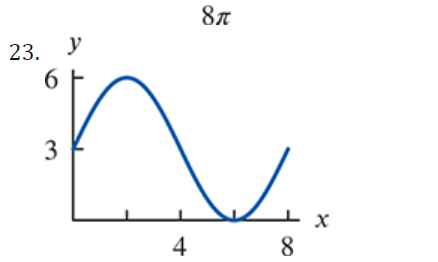

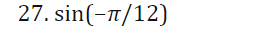
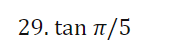
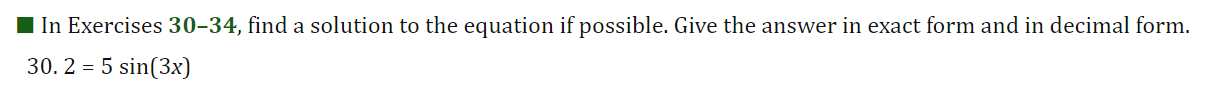
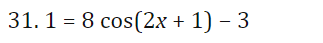
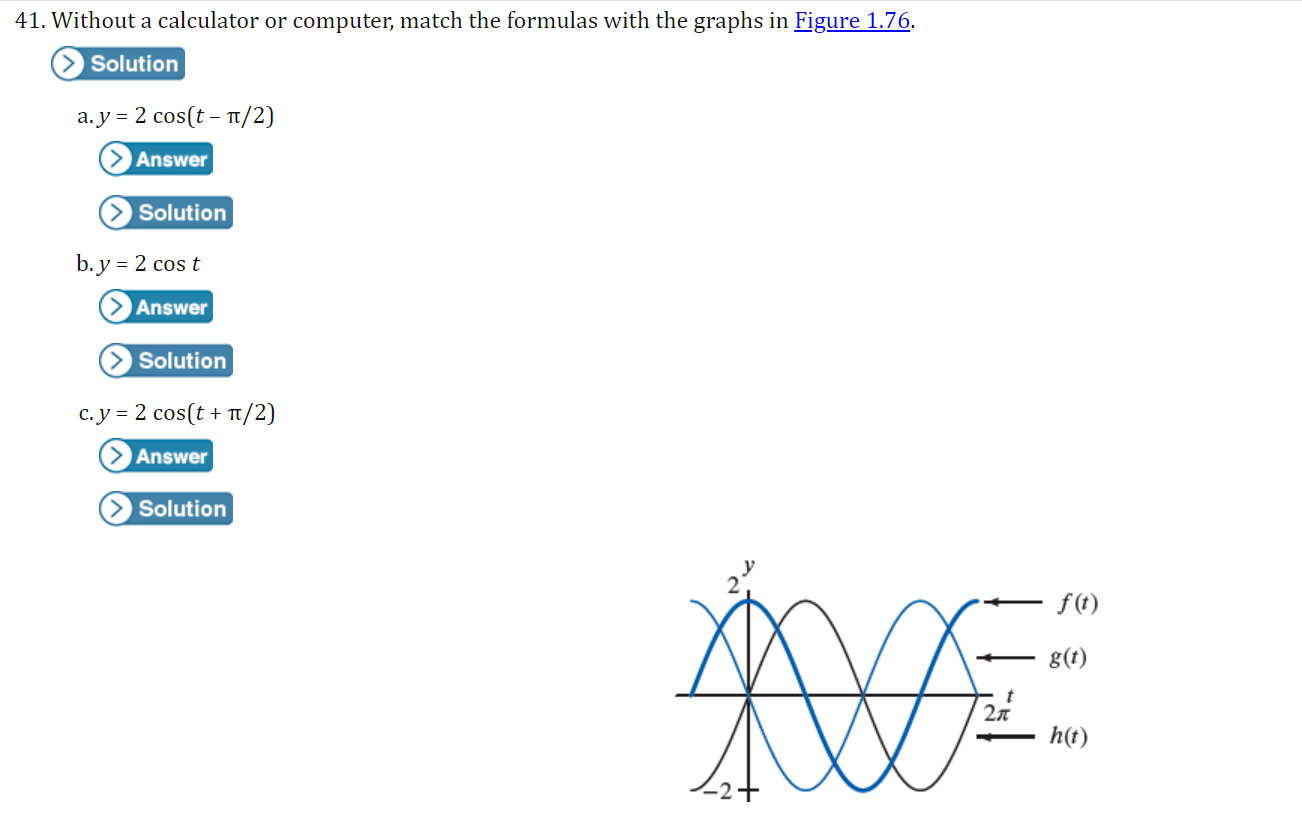
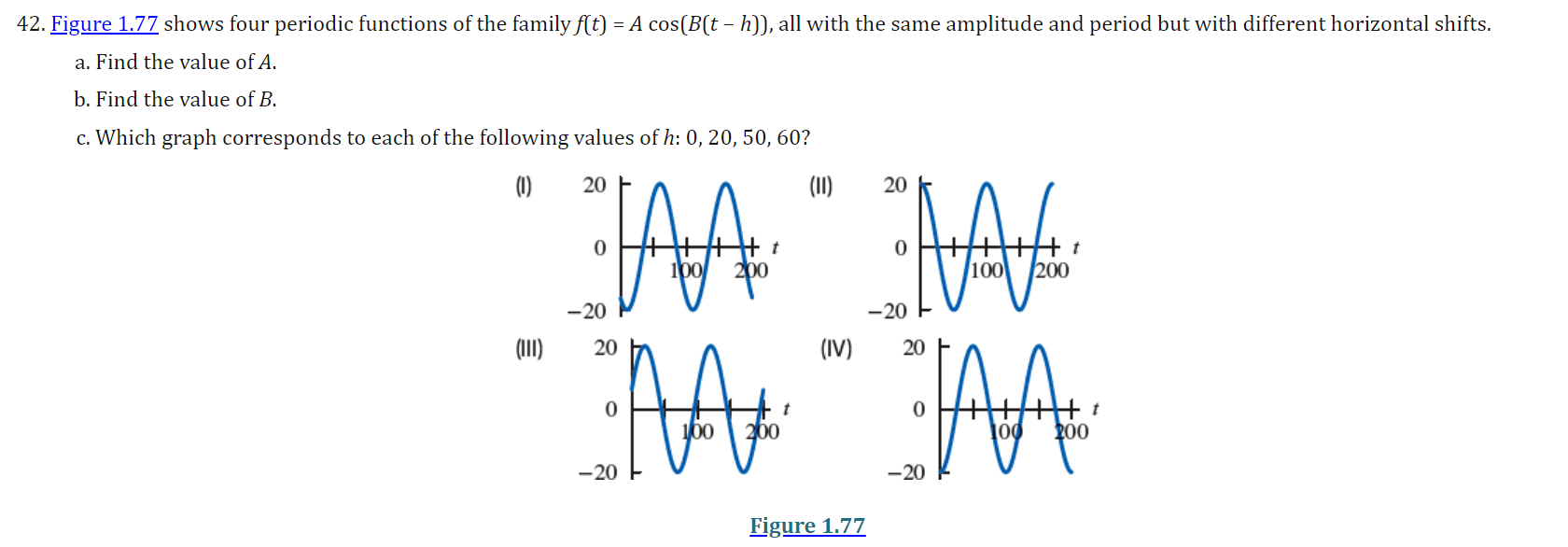

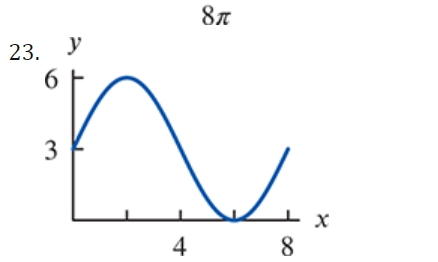
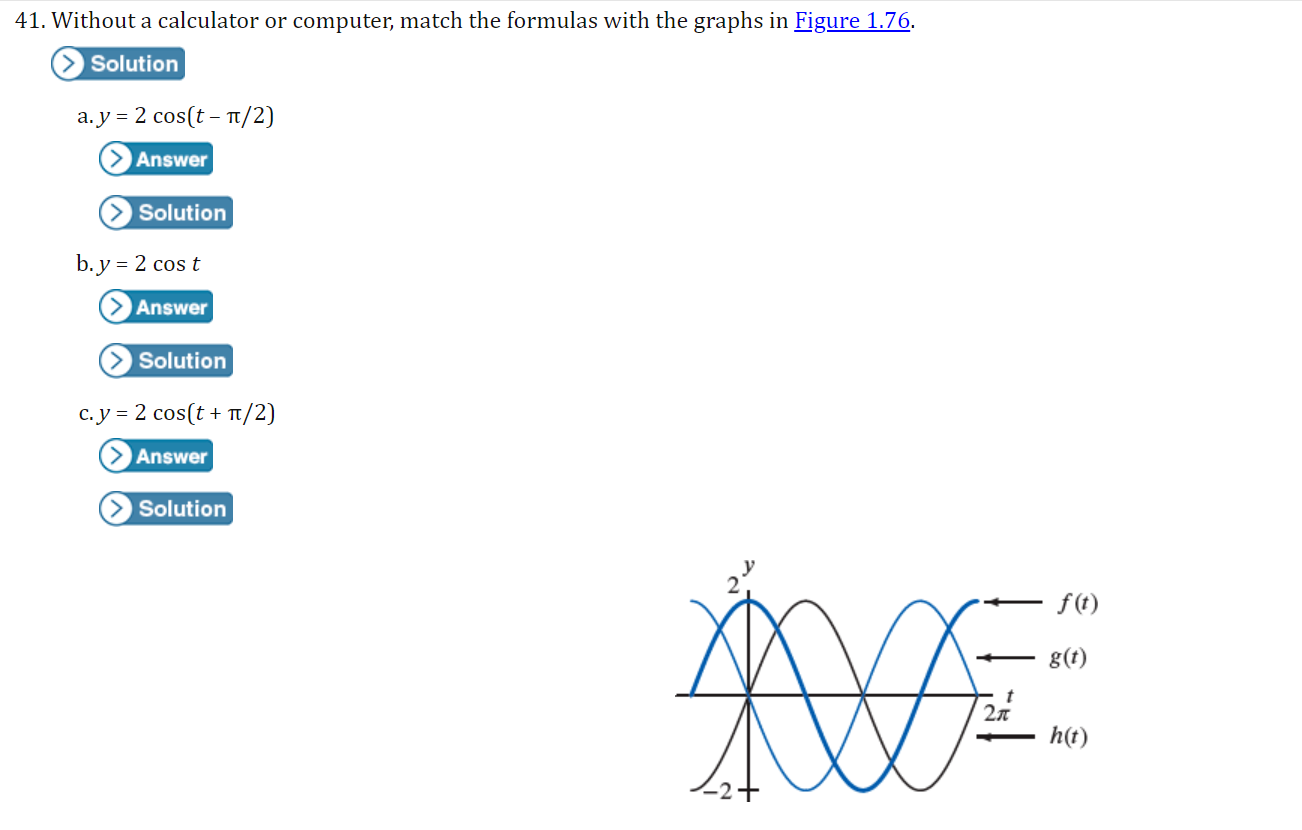
I For Exercises 19, draw the angle using a ray through the origin, and determine whether the sine, cosine, and tangent of that angle are positive, negative, zero, or undefined. Find the period and amplitude in Exercises 10-13. 10. y = 7 sin(3t)I In Exercises 2429, calculate the quantity without using the the trigonometric functions on a calculator You are given that sin(7I/12] : 0.259 and cos [11/5] : 0.809. You may want to draw a picture showing the angles involved. 24 ( .) .cos 5 27. sin 12\fI In Exercises 3034, find a solution to the equation if possible. Give the answer in exact form and in decimal form. 30. 2 : 5 sin(3X] \f41. Without a calculator or computer, match the formulas with the graphs in Figure 1.76. Solution a. y = 2 cos(t - It/2) > Answer Solution b. y = 2 cost Answer > Solution c. y = 2 cos(t + nt/2) >Answer Solution42. Figure 1.77 shows four periodic functions of the family f(t) = A cos(B(t - h)), all with the same amplitude and period but with different horizontal shifts. a. Find the value of A. b. Find the value of B. c. Which graph corresponds to each of the following values of h: 0, 20, 50, 60? (1) 20 (11) -20 (III) 20 (IV) 20 0 -20 -20 Figure 1.7769. For a boat to float in a tidal bay, the water must be at least 2.5 meters deep. The depth of water around the boat, d(t), in meters, where t is measured in hours since midnight, is d(t) = 5 + 4.6 sin (0.5t). a. What is the period of the tides in hours? > Answer > Solution b. If the boat leaves the bay at midday, what is the latest time it can return before the water becomes too shallow? > Answer > Solution 70. The Bay of Fundy in Canada has the largest tides in the world. The difference between low and high water levels is 15 meters (nearly 50 feet). At a particular point the depth of the water, y meters, is given as a function of time, t, in hours since midnight by y = D + A cos (B(t - C)). a. What is the physical meaning of D? b. What is the value of A? c. What is the value of B? Assume the time between successive high tides is 12.4 hours. d. What is the physical meaning of C
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


