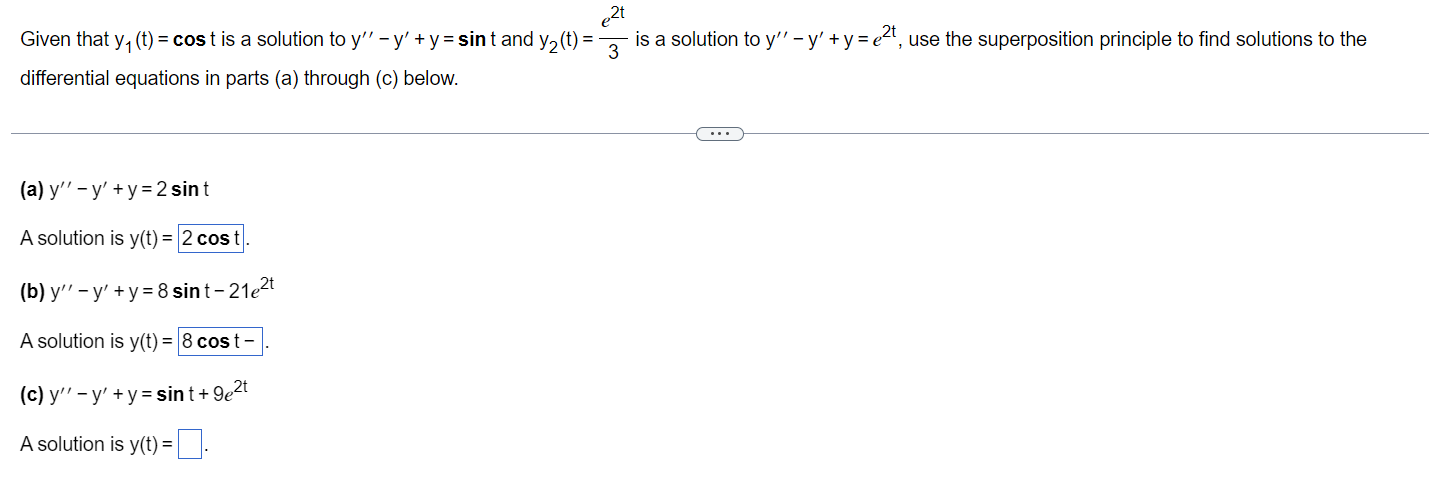
2t Given that y, (t) = cost is a solution to y" - y' + y = sin t and y, (t) = 3 is a solution to y" - y' + y = ed, use the superposition principle to find solutions to the differential equations in parts (a) through (c) below. . . . (a) y" - y' ty =2 sint A solution is y(t) = 2 cost. (b) y" - y' + y=8 sint -21e2t A solution is y(t) = 8 cost - (c) y" - y' + y= sint+ 9e2t A solution is y(t) =.Solve the given initial value problem. y" - 5y' + 4y = 0; y(0) = 1, y'(0) = - The solution is y(t) = 4t N / W e