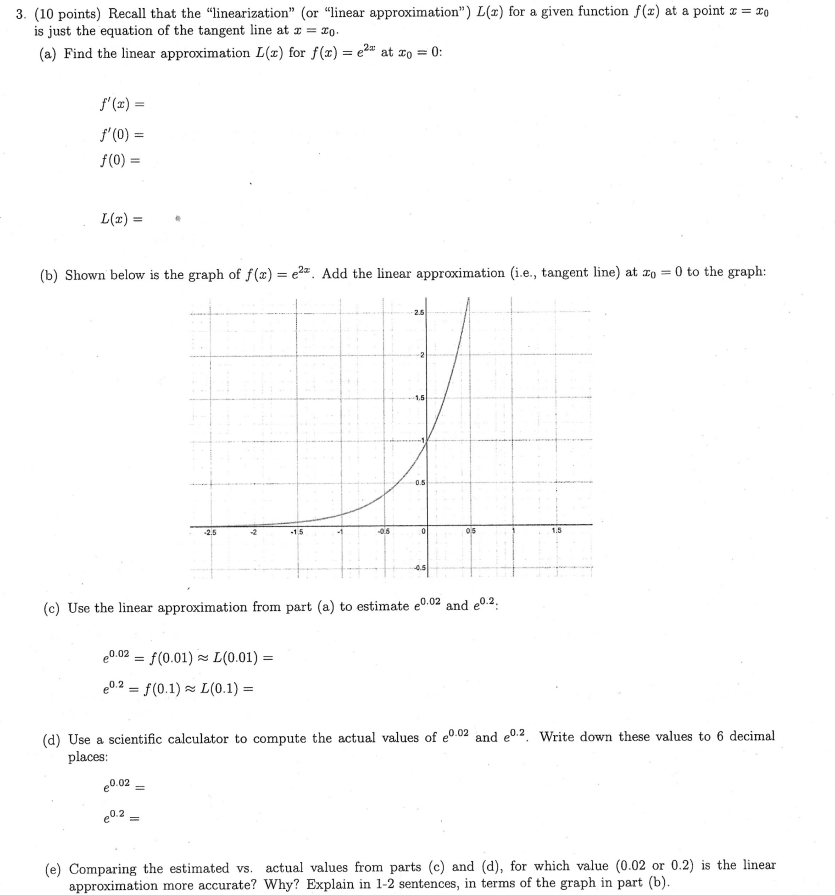
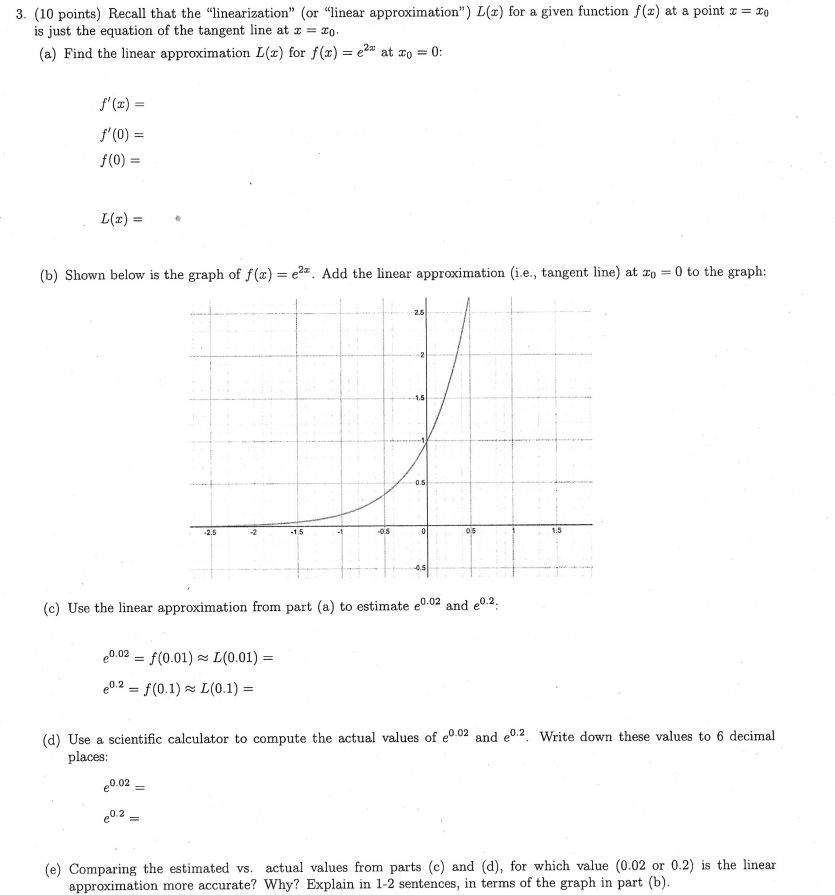
3. (10 points) Recall that the "linearization" (or "linear approximation") L(x) for a given function f(x) at a point a = To is just the equation of the tangent line at I = Fo. (a) Find the linear approximation L(x) for f (x) = ezz at To = 0: f'(x) = f'(0) = f (0) = L(x) = (b) Shown below is the graph of f(x) = e . Add the linear approximation (i.e., tangent line) at zo = 0 to the graph: (c) Use the linear approximation from part (a) to estimate e0 02 and e0.2. 0.02 = f (0.01) ~ L(0.01) = 20.2 = f(0.1) = L(0.1) = (d) Use a scientific calculator to compute the actual values of e"- and e. Write down these values to 6 decimal places: 0.02 = (e) Comparing the estimated vs. actual values from parts (c) and (d), for which value (0.02 or 0.2) is the linear approximation more accurate? Why? Explain in 1-2 sentences, in terms of the graph in part (b)