Question: Use linear approximation to approximate v64.4 as follows. Let f(@) = Va. The equation of the tangent line to f(x) at a = 64 can


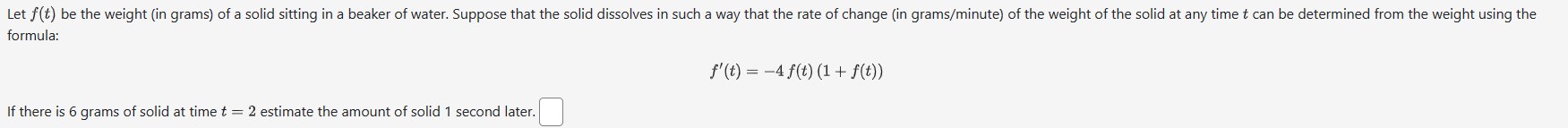
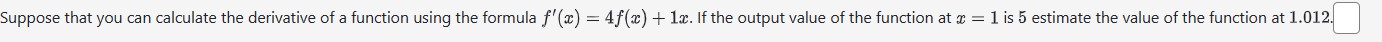
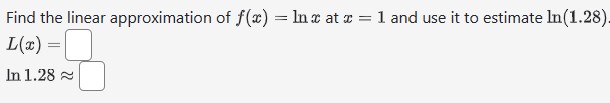


![estimate K12): C] Let f(t) be the weight (in grams) of a](https://s3.amazonaws.com/si.experts.images/answers/2024/06/666136627ab12_946666136624812b.jpg)
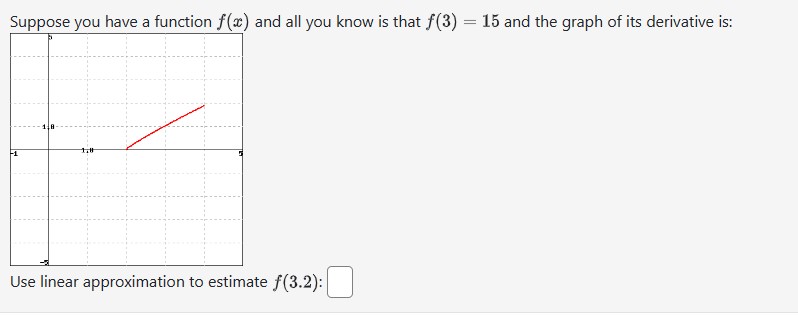
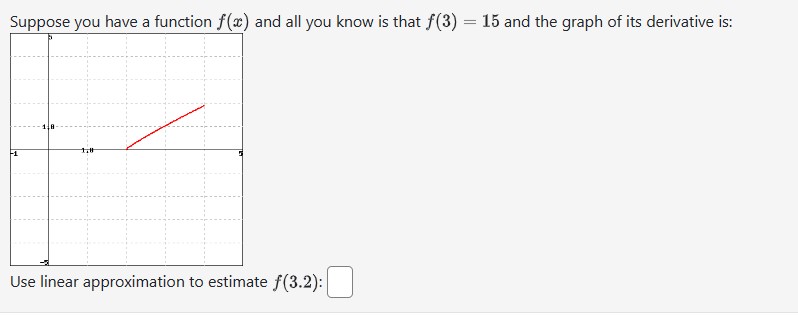
Use linear approximation to approximate v64.4 as follows. Let f(@) = Va. The equation of the tangent line to f(x) at a = 64 can be written in the form y = ma + b. Compute m and b. m b Using this find the approximation for V64.4. Answer:Use linear approximation, i.e. the tangent line, to approximate 3.85 as follows: Let x} : $5. The equation of the tangent line to re} at a: i 4 can be written in the form 1; 2 mm + I5 where m. is: and where b is: |_l Using this, we find our approximation for 385 is D Suppose you have a function at) and all you know is that f(3} = 15 and the graph of its derivative is: Use linear approximation to estimate K12): C] Let f(t) be the weight (in grams) of a solid sitting in a beaker of water. Suppose that the solid dissolves in such a way that the rate of change (in grams/minute) of the weight of the solid at any time t can be determined from the weight using the formula: f' (t ) = - 4f (t ) (1 + f (t ) ) If there is 6 grams of solid at time t = 2 estimate the amount of solid 1 second later.Suppose that you can calculate the derivative ofa function using the formula fr(w) = 4f(m} + 13:. If the output value of the function at w = 1 is 5 estimate the value of the function $13128 Find the linear approximation of x) = 1:19: at m = 1 and use it to estimate 1:0.(128). L(a:) 2r 1111.289
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


