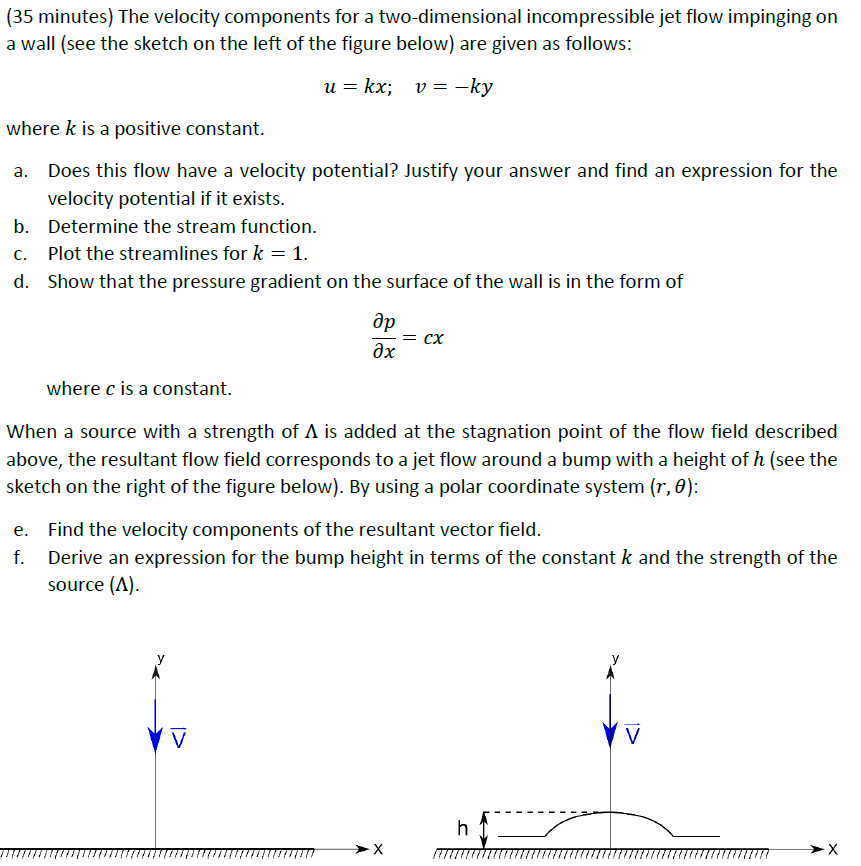
Question: ( 3 5 minutes ) The velocity components for a two - dimensional incompressible jet flow impinging on a wall ( see the sketch on
minutes The velocity components for a twodimensional incompressible jet flow impinging on a wall see the sketch on the left of the figure below are given as follows:
uk x ; quad vk y
where k is a positive constant.
a Does this flow have a velocity potential? Justify your answer and find an expression for the velocity potential if it exists.
b Determine the stream function.
c Plot the streamlines for k
d Show that the pressure gradient on the surface of the wall is in the form of
fracpartial ppartial xc x
where c is a constant.
When a source with a strength of Lambda is added at the stagnation point of the flow field described above, the resultant flow field corresponds to a jet flow around a bump with a height of h see the sketch on the right of the figure below By using a polar coordinate system rtheta :
e Find the velocity components of the resultant vector field.
f Derive an expression for the bump height in terms of the constant k and the strength of the source Lambda
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


