$374$

Chapter $20$ Model Predictive Control

The predicted unforced response hat$(y)(k+J)$ can be calculated from Eq$.20-19$ with $j=J.$

The control law in Eq$.20-22$ is based on a single prediction that is made for $J$ steps in the future. Note that the control law can be interpreted as the inverse of the predictive model in Eq$.20-21.$

EXAMPLE $20\mathrm{.}3$

Apply the predictive control law of Example $20\mathrm{.}2$ to a fifth$-$order process:

$\frac{Y(s)}{U(s)}=\frac{1}{(5s+1{)}^5}$

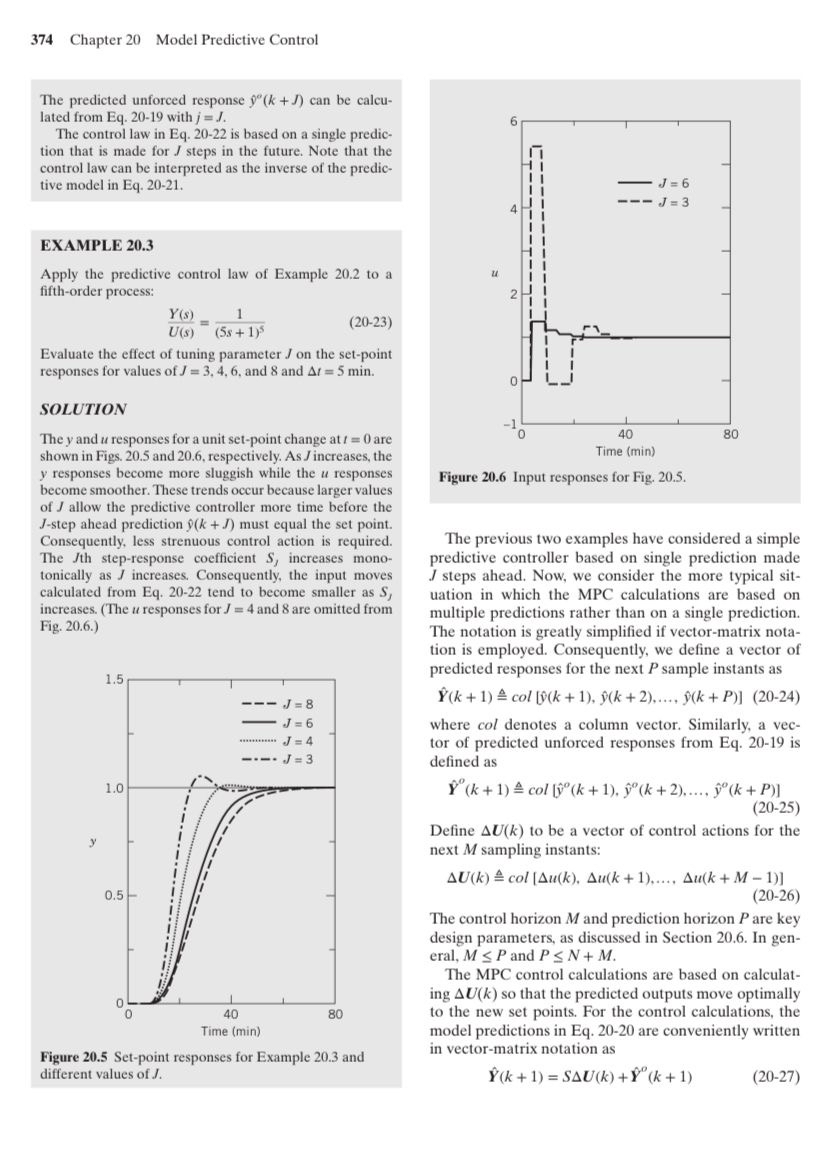
Evaluate the effect of tuning parameter $J$ on the set$-$point responses for values of $J=3,4,6,$ and $8$ and $t=5$min.

SOLUTION

The $y$ and $u$ responses for a unit set$-$point change at $t=0$ are shown in Figs. $20\mathrm{.}5$ and $20\mathrm{.}6,$ respectively. As $J$ increases, the $y$ responses become more sluggish while the $u$ responses become smoother. These trends occur because larger values of $J$ allow the predictive controller more time before the $J-$step ahead prediction hat$(y)(k+J)$ must equal the set point. Consequently, less strenuous control action is required. The $J$ th step$-$response coefficient $S_j$ increases monotonically as $J$ increases. Consequently, the input moves calculated from Eq$.20-22$ tend to become smaller as $S_j$ increases. $($The $u$ responses for $J=4$ and $8$ are omitted from Fig. $20\mathrm{.}6.)$ different values of $J.$

F

The previous two examples have considered a simple predictive controller based on single prediction made $J$ steps ahead. Now, we consider the more typical situation in which the MPC calculations are based on multiple predictions rather than on a single prediction. The notation is greatly simplified if vector$-$matrix notation is employed. Consequently, we define a vector of predicted responses for the next $P$ sample instants as

hat$(Y)(k+1)col[hat(y)(k+1),$hat$(y)(k+2),$dots,hat$(y)(k+P)]$

where col denotes a column vector. Similarly, a vector of predicted unforced responses from Eq$.20-19$ is defined as

hat$(Y{)}^o(k+1)col[hat(y{)}^o(k+1),$hat$(y{)}^o(k+2),$dots,hat$(y{)}^o(k+P)]$

Define $U(k)$ to be a vector of control actions for the next $M$ sampling instants:

$U(k)col[u(k),u(k+1),$dots,$u(k+M-1)]$

The control horizon $M$ and prediction horizon $P$ are key design parameters, as discussed in Section $20\mathrm{.}6.$ In general, $MP$ and $PN+M.$

The MPC control calculations are based on calculating $U(k)$ so that the predicted outputs move optimally to the new set points. For the control calculations, the model predictions in Eq$.20-20$ are conveniently written in vector$-$matrix notation as

Solve the answer using similunk showing the indication