3 Assignment Tasks 3.1 Ordinary Differential Equations If you are using You are required to implement four one-step-methods in fully annotated MATLAB/ Octave or Python functions. If you are to submit your work using MATLAB/Octave you should submit the codes detailed in Section 3.1.1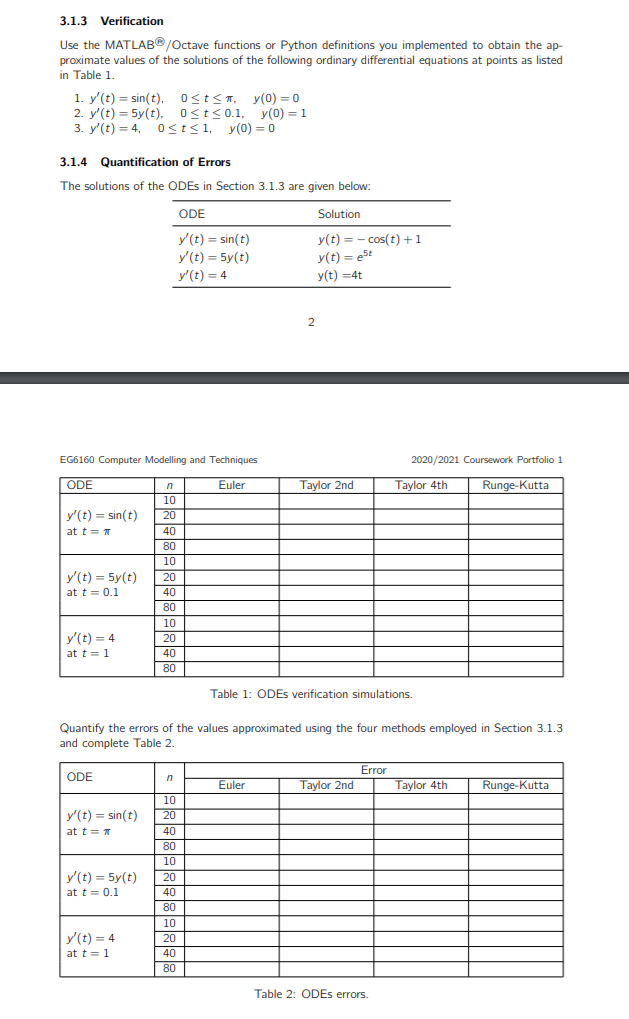

3.1.1 MATLAB/Octave If you are using MATLAB/Octave, you are required to submit the following functions with the specified declarations of function names, input and output parameters. Method Function Declaration Euler function y = euler( f, y0, t ) 2nd Order Taylor function y = Taylor2(f, fp, y0, t) 4th Order Taylor function y = Taylor4(f, fp, fpp, fppp, y0, t) Runge-Kutta function y = RungeKutta (f, y0, t) Where t is the time array, y0 boundary condition at t0, f is the differential equation to be integrated; fp, fpp, and fppp are the first, second and third derivatives of fp, respectively.

3.1.3 Verification Use the MATLAB/Octave functions or Python definitions you implemented to obtain the ap- proximate values of the solutions of the following ordinary differential equations at points as listed in Table 1. 1. y' (t) = sin(t). Ost