3

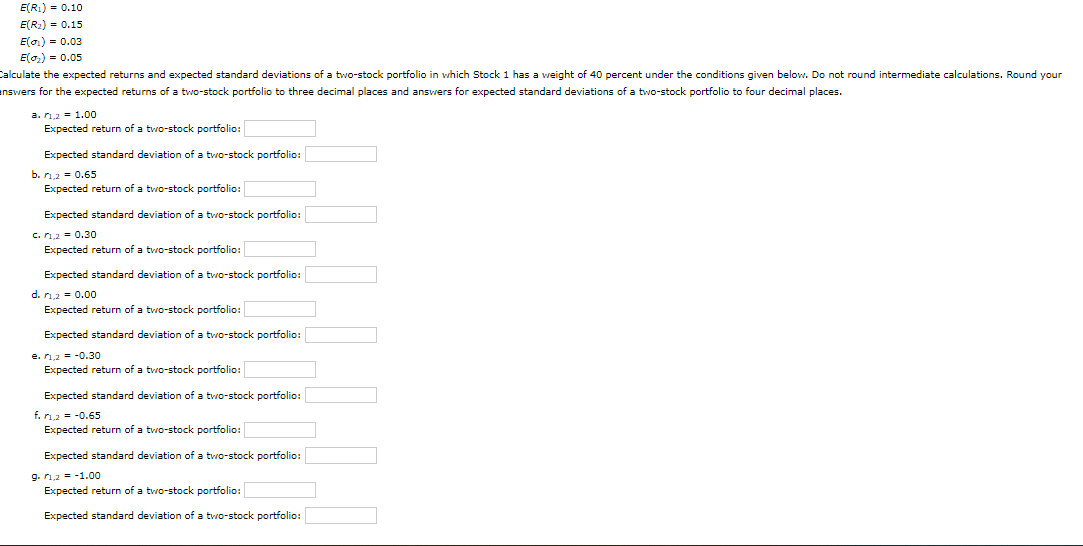
E(R) = 0.10 E(R2) = 0.15 EO) = 0.03 E(0) = 0.05 Calculate the expected returns and expected standard deviations of a two-stock portfolio in which Stock 1 has a weight of 40 percent under the conditions given below. Do not round intermediate calculations. Round your answers for the expected returns of a two-stock portfolio to three decimal places and answers for expected standard deviations of a two-stock portfolio to four decimal places. a. 1.2 = 1.00 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: b. n2 = 0.65 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: c. 12 = 0.30 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: d. n = 0.00 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: e. 12 = -0.30 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: f.n2 = -0.65 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio: 9. 12 = -1.00 Expected return of a two-stock portfolio: Expected standard deviation of a two-stock portfolio