(3) Find the function that approximates\

f(hat(x))=(1)/(1+x^(2))

\ when

x

is near

x=0

.\ (4)\

T=2\\\\pi \\\\sqrt((l)/(g))

\ where

g

is constant. If

\\\\Delta T(l)=T(l+\\\\Delta l)-T(l)

show that\

\\\\Delta T(l)~~(T)/(2l)\\\\Delta l

\ when

\\\\Delta l

is small.

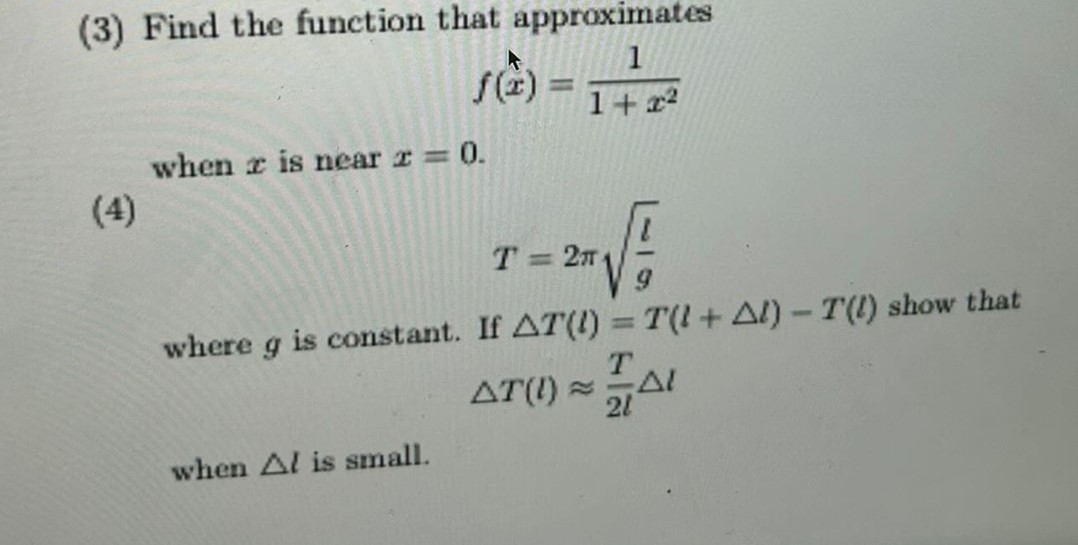
(3) Find the function that approximates f(x^)=1+x21 when x is near x=0. (4) T=2gl where g is constant. If T(l)=T(l+l)T(l) show that T(l)2lTl when l is small