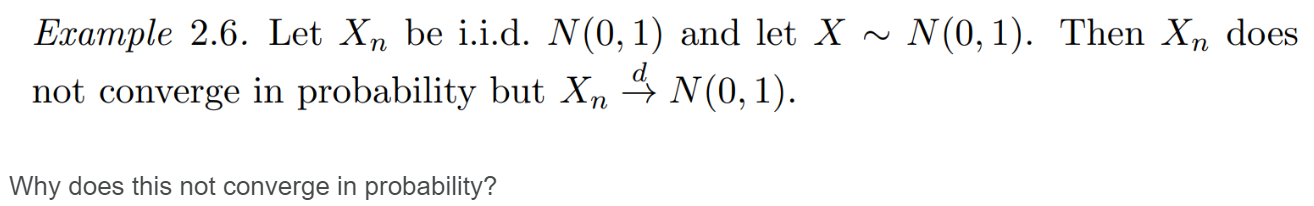
3. Let X, Y i.i.d. U(0, 1) random variable. (a) Compute P(|X Y| ) for < 1. Hint: Set up a double integral. (b) Let X1, X2,... be i.i.d. U(0, 1) random variables. Using (a), or otherwise, argue that n does not converge in probability to any random variable. Hint: See the discussion Example 2.6. Let Xn be i.i.d. N(0, 1) and let X not converge in probability but X 4 N(0, 1). Why does this not converge in probability? ~ N(0, 1). Then X does P Suppose Xn X for some X. When n is large, we have that is close to X with high probability. This implies that if n, m are both large, then n should be close to Xm with high probability (as both are close to ). But this is impossible since X and Xm are independent N(0, 1) random variables. n This is related to the idea of "Cauchy sequence" in real analysis.