Question: 3 sin (n) 2. Consider the sequence n=1 (a) (10 points) Prove that the sequence above converges to 0. (b) (10 points) Prove that

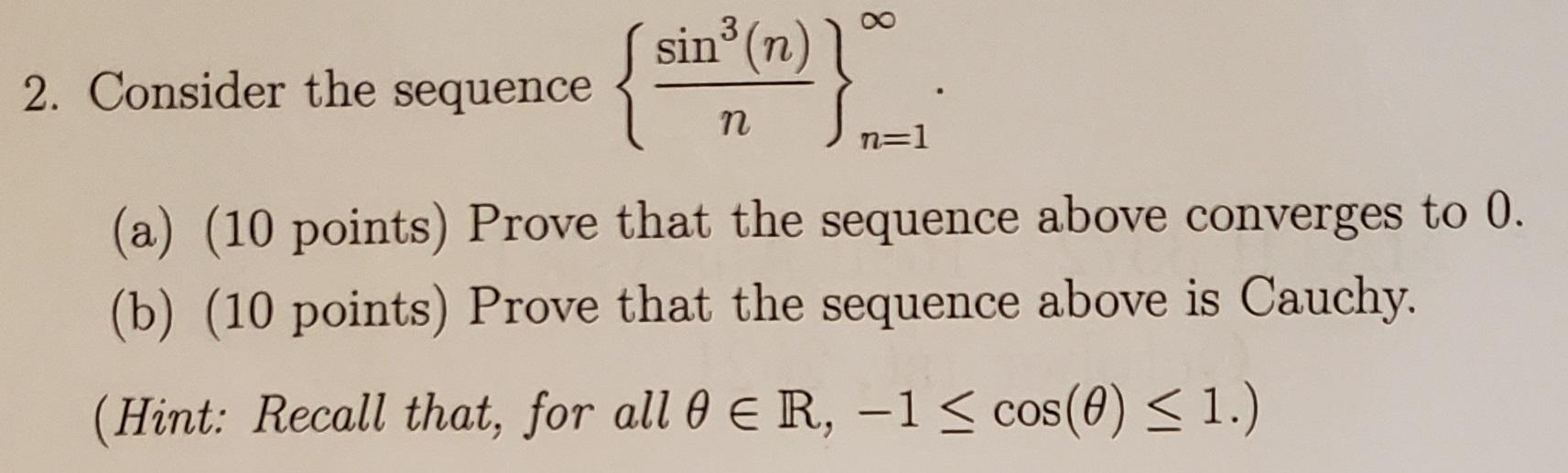
3 sin (n) 2. Consider the sequence n=1 (a) (10 points) Prove

3 sin (n) 2. Consider the sequence n=1 (a) (10 points) Prove that the sequence above converges to 0. (b) (10 points) Prove that the sequence above is Cauchy. (Hint: Recall that, for all 0 E R, -1 < cos(0) < 1.) COS

Step by Step Solution

★★★★★

3.46 Rating (153 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

Solution Civen sequence Let a have we Juner limm 0 ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

Prove that r = a sin + b cos represents a circle and find its center and radius.

Prove that if a sequence converges in distribution to a constant value, then it also converges in probability. This one together constitute an alternative proof to the weak law of large numbers.

A monotone sequence in R converges if and only if it is bounded. [If xn is a bounded monotone sequence, show that xn sup{xn}.]

3. In Problem 2, consider the following changes: The processing time at the bottleneck station could be reduced by 33 per cent by investing in better technology. The cost of this improvement is...

help solve y (0, 2.1 (0, 1.9 ) (1, 2 (0.95, 0) (1.05, 0) -2 2 X + A v N f (x) = 2x X a=1 X -10 . . 10 3 f(a) X = 2 Use the graph above (click the double arrows next to the gear to enlarge the graph)...

8.1. Dulles Electric Company buys 1 million tons of coal annually to burn at its power plant. The company wants to invest in a unit train that will haul coal from the mine to the power house, where...

6.1. Carbondale Company has the following credit policy 2/10, net 30. Carbondale also charges 1% per month interest on all accounts after 30 days. The following table shows the collection schedule of...

Consider the function f (x) = 3 sin (0.6x 2). (a) Approximate the zero of the function in the interval [0, 6]. (b) A quadratic approximation agreeing with f at x = 5 is g (x) = -0.45x2 + 5.52x -...

s1 educated (SSE) student for every three public school educated (PSE) students. Reasoning that students are not very dissimilar from threads, he suggests the following entry and exit routines be...

What is the role of the potato extract in the decomposition of hydrogen peroxide in water?: Acts activating the decomposition process because it contains an enzyme called "catalase", which catalyzes...

Differentiate tan(7x+9x-2.5)

Explain the sources of recruitment.

Differentiate sin(5x+2)

Compute the derivative f(x)=1/ax+bx

What is the meaning of strategic management and what are their objectives and advantages of strategic management?

(1 point) Suppose that a payment in three years of 10000 dollars has a present value of 8120.57 dollars. What is the nominal rate of interest convertible quarterly? Answer = percent

The Home Depot is the leading retailer in the home improvement industry and one of the 10largest retailers in the United States. The company included the following on its January 29, 2012, balance...

Assume that the return R t of a stock has the following log-normal distribution for fixed t: log (Rt) ~ N(, 2 ). Suppose we let the density of log(R t ) be denoted by f(R t ) and hypothesize that =...

The long rate R and the short rate r are known to have a jointly normal distribution with variance-covariance matrix ? and mean ?. These moments are given by Let the corresponding joint density be...

In this exercise we use the Girsanov theorem to price the chooser option. The chooser option is an exotic option that gives the holder the right to choose, at some future date, between a call and a...

To what extent has the network management approach helped Benetton to prosper in difficult trading conditions in Europe? What have been the gains for stakeholders?

Think of a market relationship that you have currently in which the intentions of the provider are more sophisticated than mere persuasion. What do they gain from this? Ask them if you cannot answer...

It is reported that corporations can save large sums of money by enabling people to use the Internet more. Suggest ways in which this might work, and identify implications for communication managers...