Question: 3. When learning fraction division, students are often told to just memorize the algorithm keep, change, flip where you keep the first fraction, change the

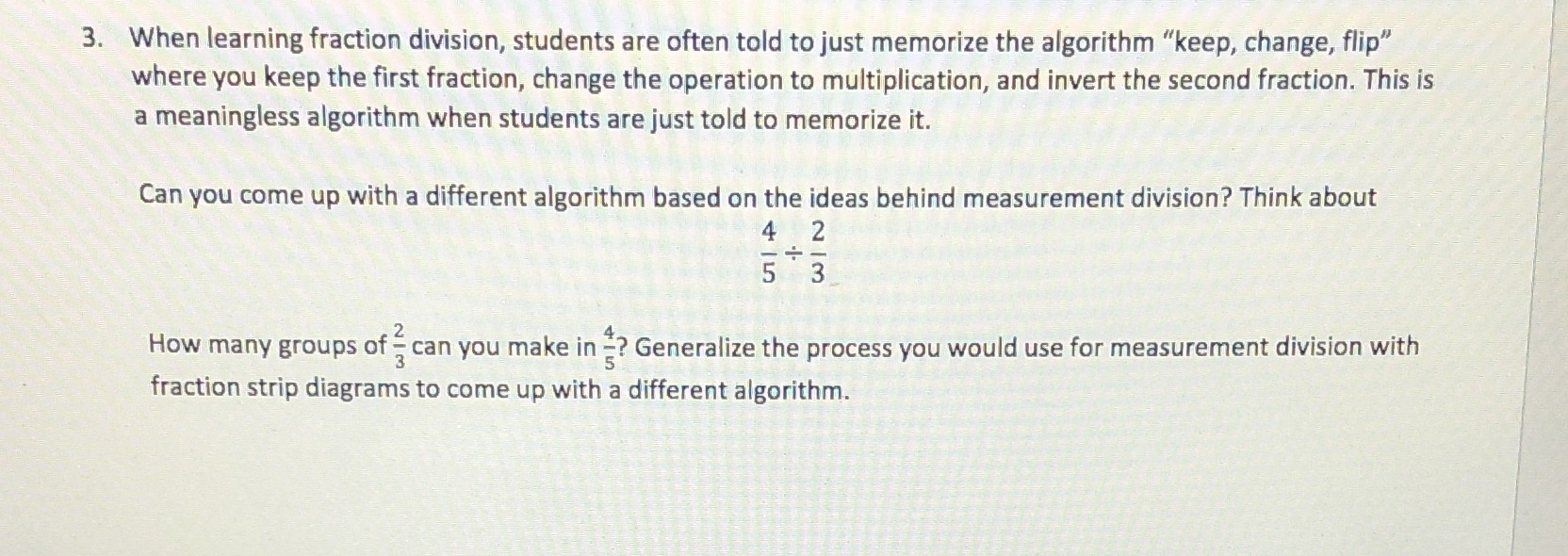
$3. When learning fraction division, students are often told to just$

3. When learning fraction division, students are often told to just memorize the algorithm "keep, change, flip" where you keep the first fraction, change the operation to multiplication, and invert the second fraction. This is a meaningless algorithm when students are just told to memorize it. Can you come up with a different algorithm based on the ideas behind measurement division? Think about WIN How many groups of = can you make in ? Generalize the process you would use for measurement division with fraction strip diagrams to come up with a different algorithm

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

#2 please! 2. Write a short "story problem" that models the division 2- = =. Is the answer to your question really 2 - + 2? Did you write a measurement or a partitive division problem? Can you write...

9/14/10 12:39 PM Page 381 Chapter dug84356_ch06a.qxd 6 Rational Expressions Advanced technical developments have made sports equipment faster, lighter, and more responsive to the human body. Behind...

MATHEMATICIANS RISE TO A CHALLENGE ne of the theorems we teach in eighth grade is a + b= *, where c is the length of the hypotenuse of a right triangle in Euclidean space, and a and b are the lengths...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

UNIT 5 QZ, Q-20 UNIT 5 / UNIT 8 QUESTIONS KEEP ANSWERS SEPARATE BY UNITS UNIT II STUDY GUIDE Consumer Mathematics Reading Assignment See information below. Key Terms 1. Add-on interest method 2....

A. B. A. B. ( ( ) ) Beginning and Intermediate Algebra An open source (CC-BY) textbook Available for free download at: http://wallace.ccfaculty.org/book/book.html by Tyler Wallace 1 ISBN...

Please be serious to my work or you don't need to accept it. Here is the requirement and Case study you need to read about. Thank you ISSUES IN ACCOUNTING EDUCATION Vol. 28, No. 3 2013 pp. 599-615...

need help with the following program reach out if you need more information. . the trace I was given the classes I was given and need help coding operator operand neg operator multiplication main...

Please read the question Question : What are "spaced practice", "varied practice", and "interleaved practice"? Give a definition for each. Then give an example of each from your own experience as a...

(answer if you can will upvote for you!!!) 1. Assess the culture of RVPT through Scheins model. a. How has it changed over time and what impact has it had on people? 2. Discuss how RVPTs PT-centric...

Read Selected Reference 5. (a) Identify the authors example of a model in the natural sciences and of a model in OR. (b) Describe the authors viewpoint about how basic precepts of using models to do...

Derive the governing partial differential equations for E(t) and H(t) in a source-free simple conducting medium (= medium with constant E, , o). That is, you should get one second order PDE for E and...

Dwyn is in the business of song writing. Dwyn writes jingles for television advertisements. Dwyn sells a jingle for a lump sum plus a royalty each time the jingle is played on TV . Dwyn has sold a (...

Horton Manufacturing Inc. produces blinds and other window treatments for residential homes and offices. The owner is concerned about the maintenance costs for the production machinery because...