Question: 3.10 Show that a norm ||-|| on a linear space X is generated by a scalar product if and only if the parallelogram equality

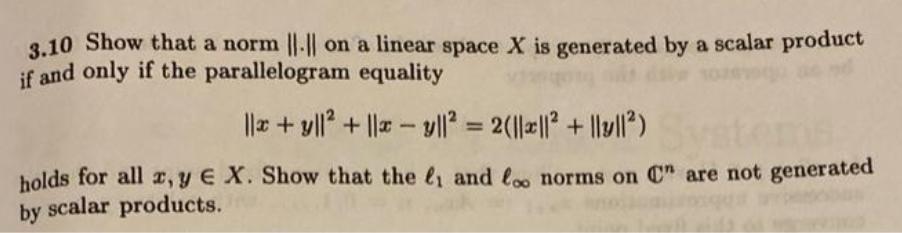
3.10 Show that a norm ||-|| on a linear space X is

3.10 Show that a norm ||-|| on a linear space X is generated by a scalar product if and only if the parallelogram equality ||x+y||+ ||xy|| = 2(||*|| + ||y||) holds for all x, y EX. Show that the and loo norms on C" are not generated by scalar products.

Step by Step Solution

★★★★★

3.29 Rating (146 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

A norm on a linear space X is generated by a scalar product if and only if the parallelogram ... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

The temperature is not 90 if and only if the air conditioner is not working, or the apartment is not hot. Write the statements in symbolic form. Let p: The temperature is 90. q: The air conditioner...

Show that a complex sequence is bounded if and only if the two corresponding sequences of the real parts and of the imaginary parts are bounded.

Show that A -1 exists if and only if the eigenvalues 1 , , n are all nonzero, and then A -1 has the eigenvalues 1/ 1 , ,1/ n .

The employee benefits expense is made up of both Rewards Income Tax CPP and El.

Functional analysis Questions 81 17:36 - Expert Q&A W + 2. A subset M of a normed space X is said to be conver if x, y e M implies that { z EX : 2 = ax + ( 1 - c ) y, 0 s as1}cM, i.e. if the "line...

please help with this question 3.10 Shaw that a. norm H.\" on a. linear space X is generated by a scalar product if and only if the parallelogram equality \"I + ylln + IIT - :JI!2 : i'Elltllz...

The Basics of Financial Mathematics Spring 2003 Richard F. Bass Department of Mathematics University of Connecticut c These notes are 2003 by Richard Bass. They may be used for personal use or class...

Probability and Statistics - Problem Set c Keith M. Chugg October 2, 2015 1 Preliminaries, Combinatorics, Set Probability 1.1. A number of bats are in a cave. 2 bats can see out of their left eye. 3...

https://www.canny-creative.com/rebranding-failures-how-much-they-cost/ Identify at least TWO reasons on why brands discussed in the article have not enjoyed a successful transition from the new brand...

Management theory in the 21st have elements of classical management theories. Group of answer choices True False

Ronald Fisher, an English statistician (18901962), collected measurements for a sample of 150 irises. Of concern were the following variables: species, petal width (PW), petal length, sepal width...

Neveranerror Inc. was organized on June 2, 2010, by a group of accountants to provide accounting and tax services to small businesses. The following transactions occurred during the first month of...

Question 2 Accrued Payroll has a normal balance of: Debit Credit

Using data from a national survey, the authors of the paper What Do Happy People Do? (Social Indicators Research [2008]: 565571) concluded that there was convincing evidence of an association between...

Judy is 33, unmarried and assertive. She is a graduate in political science, and involved in union activities and anti-discrimination movements. Which of the following statements do you think is more...

Youre an optician whos been asked to design a new replacement lens for cataract patients. The lens must be 5.5mm in diameter, with focal length 17 mm, and it cant be thicker than 0.8 mm. For the lens...

Discuss how reliability, maintainability, and availability are related by using an example of a product or service that you are familiar with.

Assume the same information as E17.6 and that Steffi Graf SA reports net income in 2022 of 120,000 and in 2023 of 140,000. Total holding gains (including any realized holding gain or loss) equal...

U.S. annual inflation rates." This sheet contains the annual U.S. inflation percentages from 1914 to 2006. (A) Create a histogram for this data. Include labels with the data. In regards to the actual...

Prove the Frobenius theorem in the case where A is a 2 2 matrix.

Let A be an n x n matrix and let A be an eigenvalue of A whose eigenspace has dimension k. where I where I is the k x k identity mairk. (b) Use Theorem 6.1.1 to show that is an eigenaIue of A with...

Let x1, x2, ..., xn be the roots of the Legendre polynomial Pn. If the Ai's are defined as in Exercise 15, then the quadrature formula will be exact for all polynomials of degree less than 2n. (a) If...

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (13-1) to isolate i on the left side.

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (4-2) to isolate d1 on the left side.

Require you to manipulate a formula from the inside-back cover to isolate a different variable on the left-hand side. Rearrange formula (4-2) to isolate d3 on the left side.