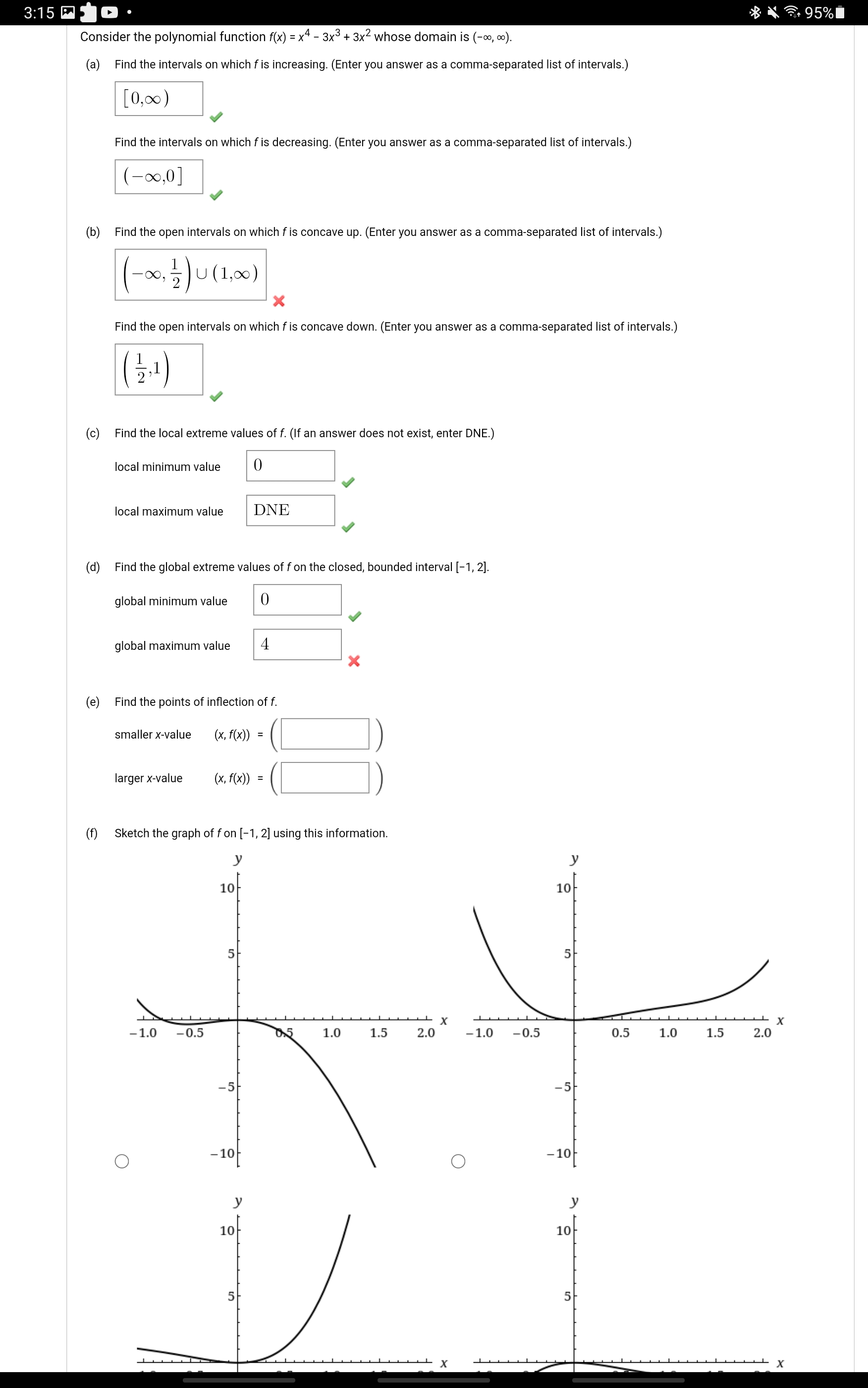
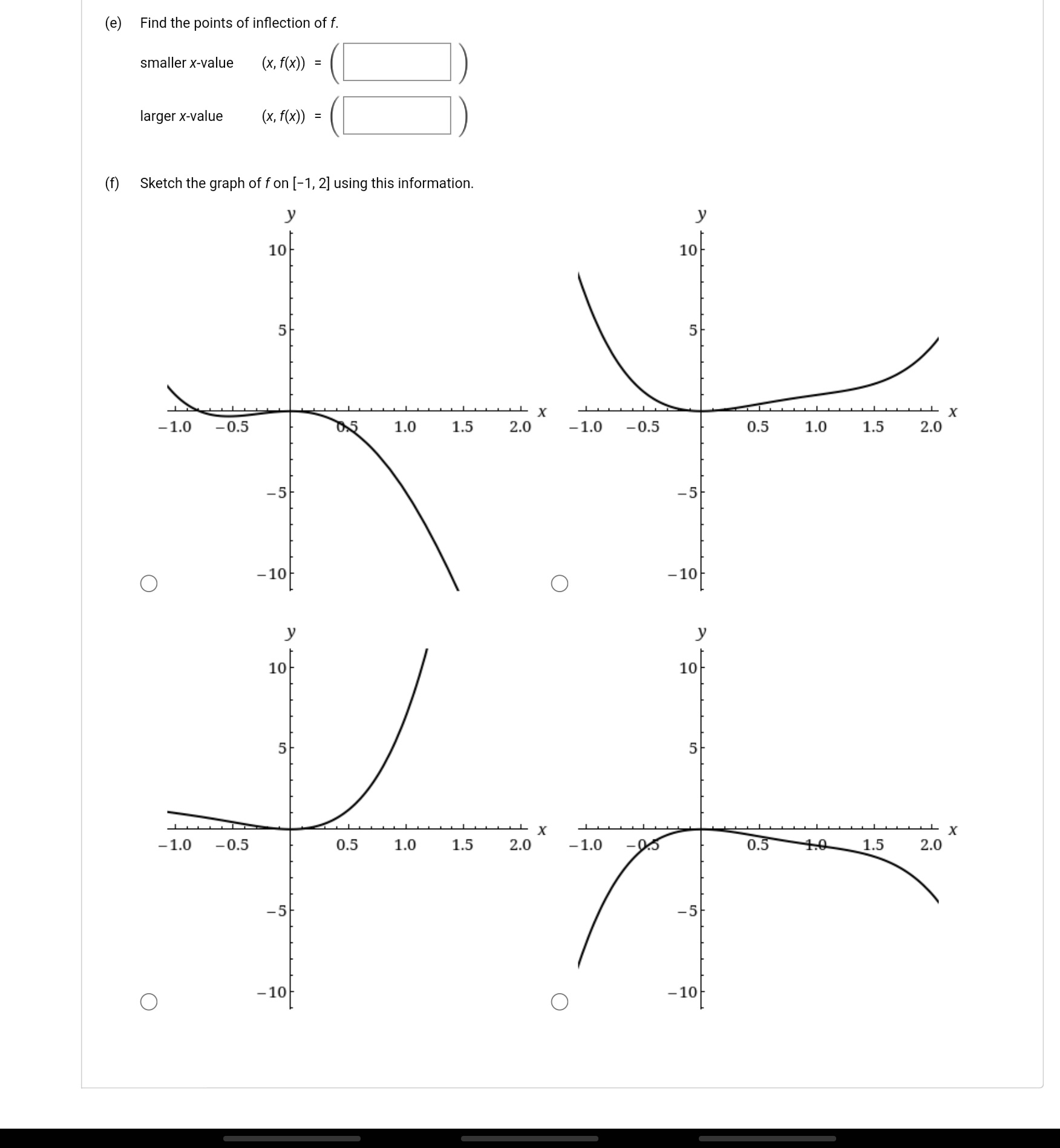
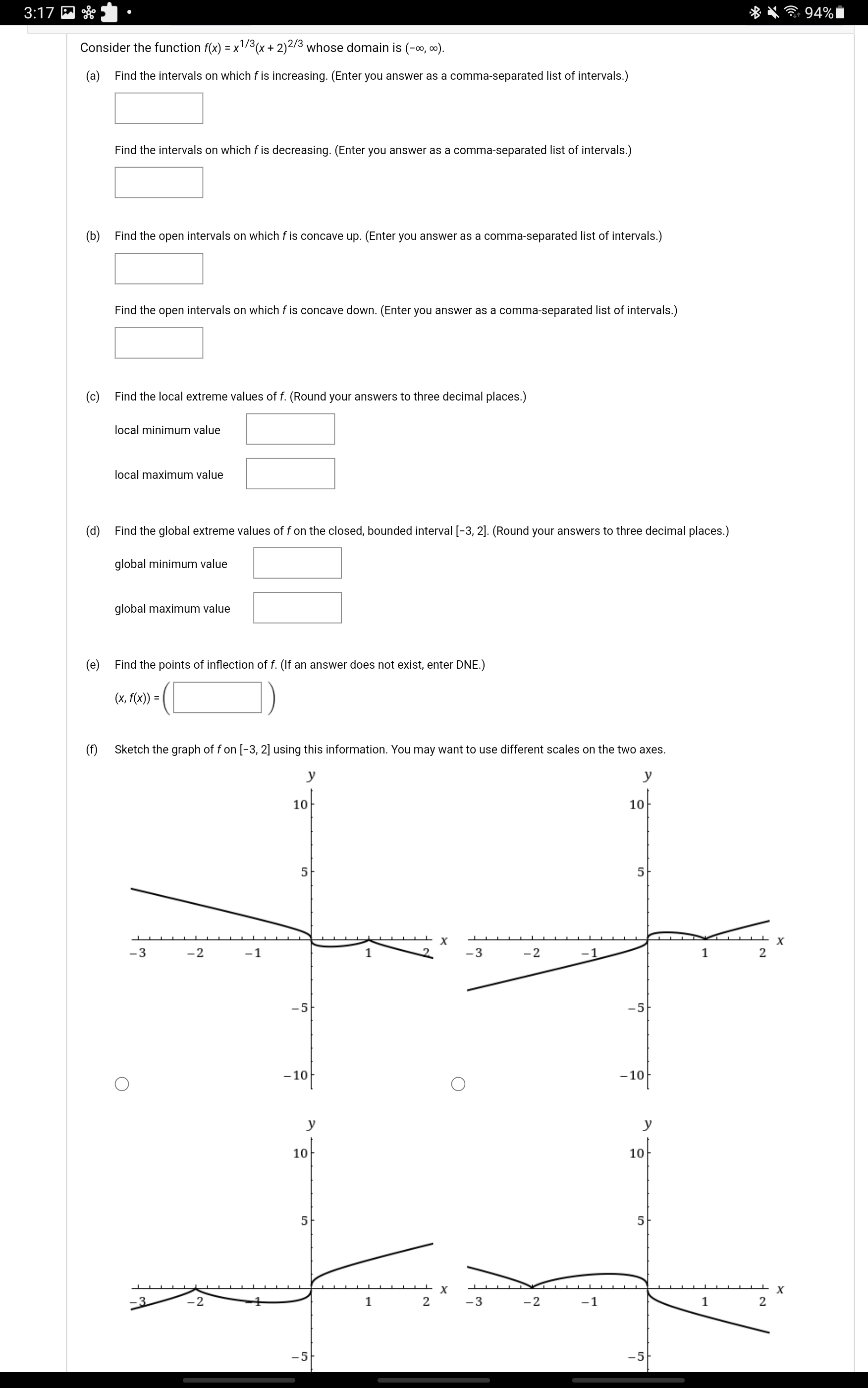
3:15 0 . B . 95% Consider the polynomial function f(x) = x# - 3x + 3x whose domain is (-0o, co). (a) Find the intervals on which f is increasing. (Enter you answer as a comma-separated list of intervals.) [0,00) Find the intervals on which f is decreasing. (Enter you answer as a comma-separated list of intervals.) (-00, 0] Find the open intervals on which f is concave up. (Enter you answer as a comma-separated list of intervals.) (-00 , 2 ) U ( 1,0 ) X Find the open intervals on which f is concave down. (Enter you answer as a comma-separated list of intervals.) d the local extreme values of f. (If an answer does not exist, enter DNE.) local minimum value 0 local maximum value DNE (d) Find the global extreme values of f on the closed, bounded interval [-1, 2]. global minimum value 0 global maximum value 4 X (e) Find the points of inflection of f. smaller x-value ( x, f (x ) ) = larger x-value ( x, f (x) ) = (f) Sketch the graph of f on [-1, 2] using this information. 10 10/ 5 - X . X -1.0 -0.5 1.0 1.5 2.0 -1.0 -0.5 0.5 1.0 1.5 2.0 -5 -5 O -10 O -10 10- 10- 5 5/ X(e) Find the points of inflection of f. smaller x-value ( x, f (x) ) = larger x-value (x, f ( x ) ) = f) Sketch the graph of f on [-1, 2] using this information. 10 10 5 5/ -1.0 -0.5 0.5 1.0 1.5 2.0 -1.0 -0.5 0.5 1.0 1.5 2.0 -5 -51 O -10 O - 10 y 10 10 51 1.0 -0.5 0.5 1.0 1.5 2.0 -1.0 - U.S ).5 1.0 1.5 2.0 -5 -51 O -10 O -103:17 % B . 94% Consider the function f(x) = x1/3(x + 2)2/3 whose domain is (-co, co). (a) Find the intervals on which f is increasing. (Enter you answer as a comma-separated list of intervals.) Find the intervals on which f is decreasing. (Enter you answer as a comma-separated list of intervals.) Find the open intervals on which f is concave up. (Enter you answer as a comma-separated list of intervals.) Find the open intervals on which f is concave down. (Enter you answer as a comma-separated list of intervals.) (c) Find the local extreme values of f. (Round your answers to three decimal places.) local minimum value local maximum value (d) Find the global extreme values of f on the closed, bounded interval [-3, 2]. (Round your answers to three decimal places.) global minimum value global maximum value (e) Find the points of inflection of f. (If an answer does not exist, enter DNE.) ( x, f( x)) = ( (f) Sketch the graph of fon [-3, 2] using this information. You may want to use different scales on the two axes. y 10 10 5 X -3 -2 -1 - 3 -2 -1 1 -5 -5 O -10 O -10 10 10 5 5 X -3 -2 1 2 -3 -2 -1 1 2 -5 -5