Question: 3.17. Let A be a square matrix with an eigenvalue c and corresponding eigen- vector v. Consider the matrix polynomial in A p( A) =

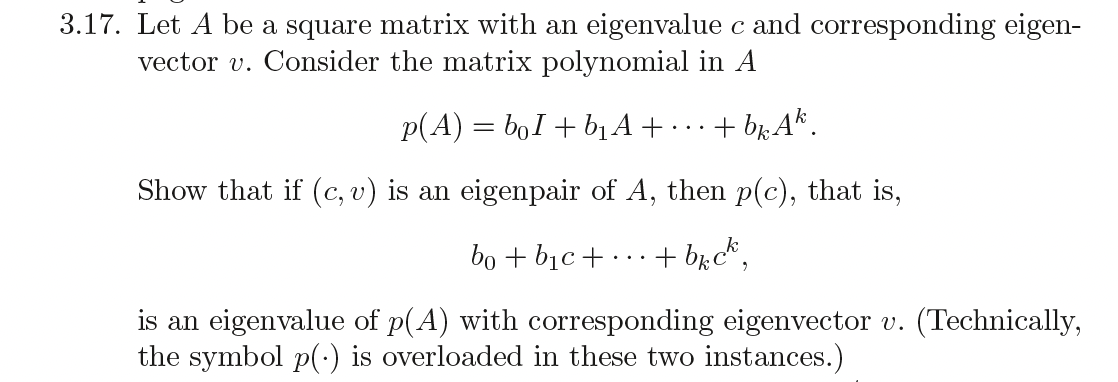
3.17. Let A be a square matrix with an eigenvalue c and corresponding eigen- vector v. Consider the matrix polynomial in A p( A) = bol+bjA + ...+ bRAk. Show that if (c, v) is an eigenpair of A, then p(c), that is, bot bict ... + back, is an eigenvalue of p(A) with corresponding eigenvector v. (Technically, the symbol p(.) is overloaded in these two instances.)

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

full step plx 5. Let A be a square matrix and A be an eigenvalue of A. Suppose u is an eigenvector of A corresponding to A. (a) Show that u is an eigenvector of A2. What is its corresponding...

7. Let A be the square matrix given by 5 O O 0 5 1 0 A = 0 0 5 1 0 0 0 5 (a) Write down the characteristic polynomial PA(x) = det(A - x14) of the matrix A. (b) Show that A has only one eigenvalue,...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Only 18 and 19 please 4.4 Eigenvalues and the Characteristic Polynomial 305 ultimately requires the evaluation of al/2 determinants of order (2 x 2). Even for modest values of n. the number a!/2 is...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials...

Can you please help me with number 31. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.7 Matrix Exponentials and Linear...

What is Exercise 32-45? I don't quite understand it, so I'm not sure if my work or answers are correct. Linear Algebra Lab Exercises Linear algebra deals with vectors and linear functions that act on...

5.1 please only write on paper. no explanation needed. Questions: 28, 33, 35 on paper 300 CHAPTER 5 Eigenvalues and Eigenvectors 26. The eigenvectors that we have been studying are sometimes called...

Can you please help me with number 12 and number 15. I have provided the math chapter it came from and the answer from the back of the book: Thank you so much and Best wishes! 5.6 Problems Find...

The following information extracts from Yoyo Bhd's financial statements: (1) Extracts from the Yoyo's statement of financial position as at 1 November 2019: RM000 Ordinary shares capital 70,000 6%...

As of January 1, Pauls Car Repair has the following accounts receivable: align="center"> Receivable Amount Due $%1,000 2,500 1,500 3,500 1,200 3,100 1,700 Days Outstanding 35 42 57 29 48 52 39...

Don't use ai and accounting question A coffee shop has a return on assets of 12%. The coffee shop's total assets amount to $350,000, while its owner's equity is $140,000 and its debt equals $210,000....

The following selected transactions relate to contingent km of Bowe Whitney Inc Bowe-Whitney's fiscal year ends on December 31. 2016, end financial statements are published in March 2017....