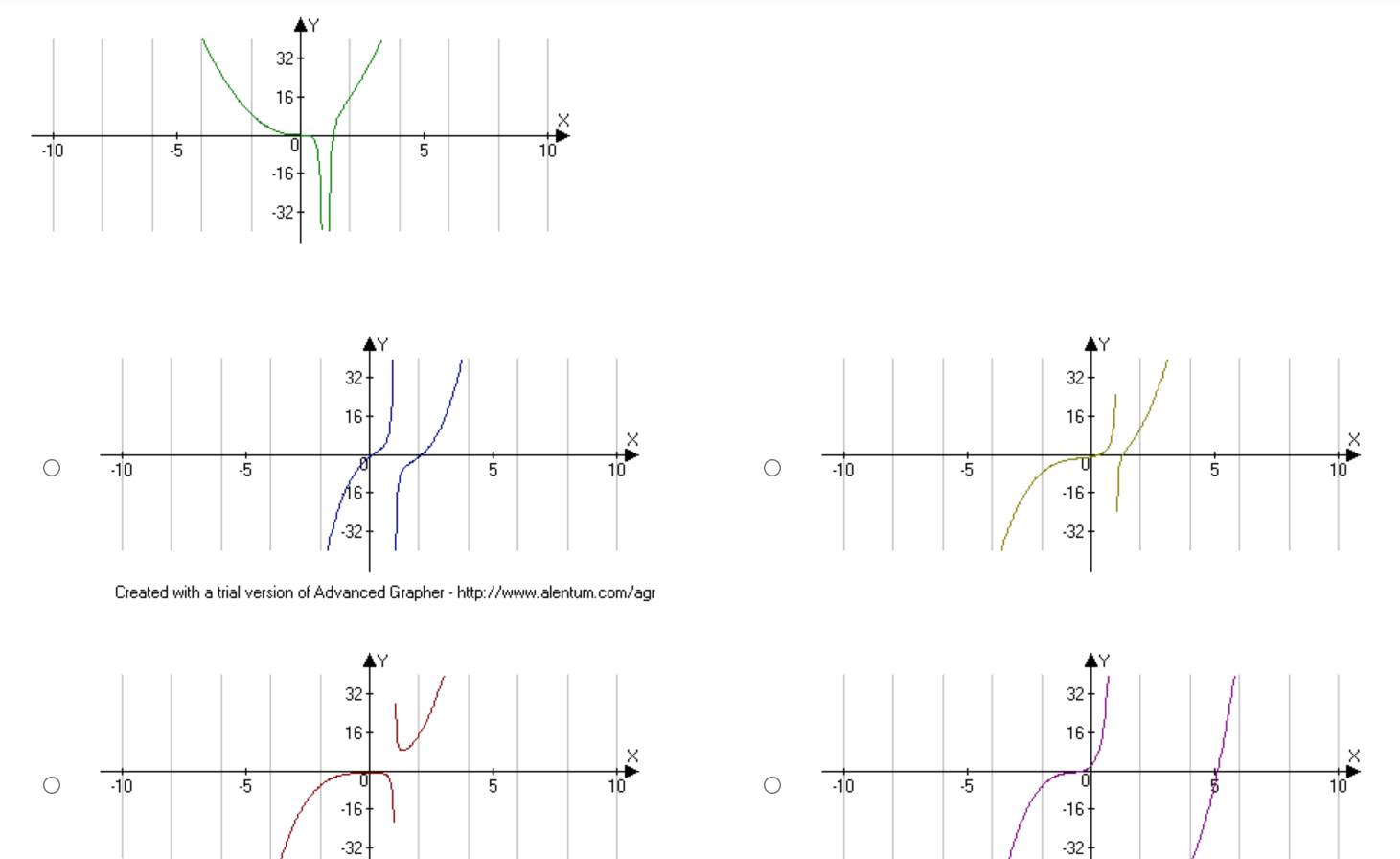
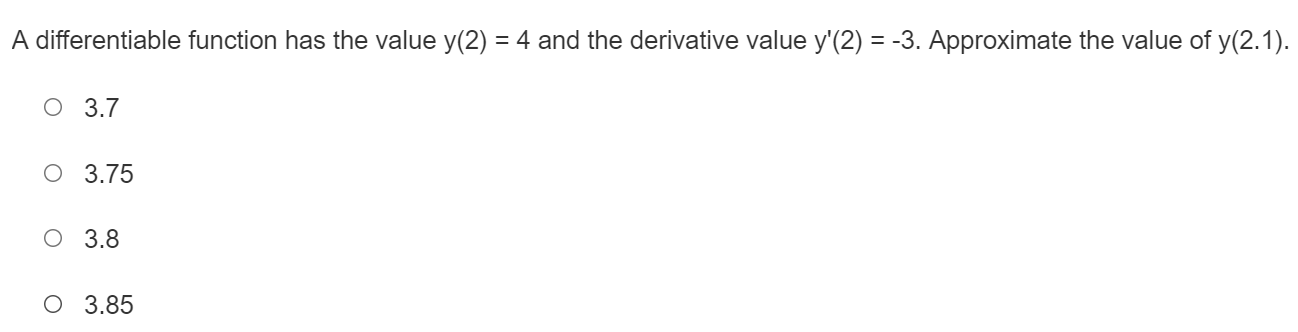
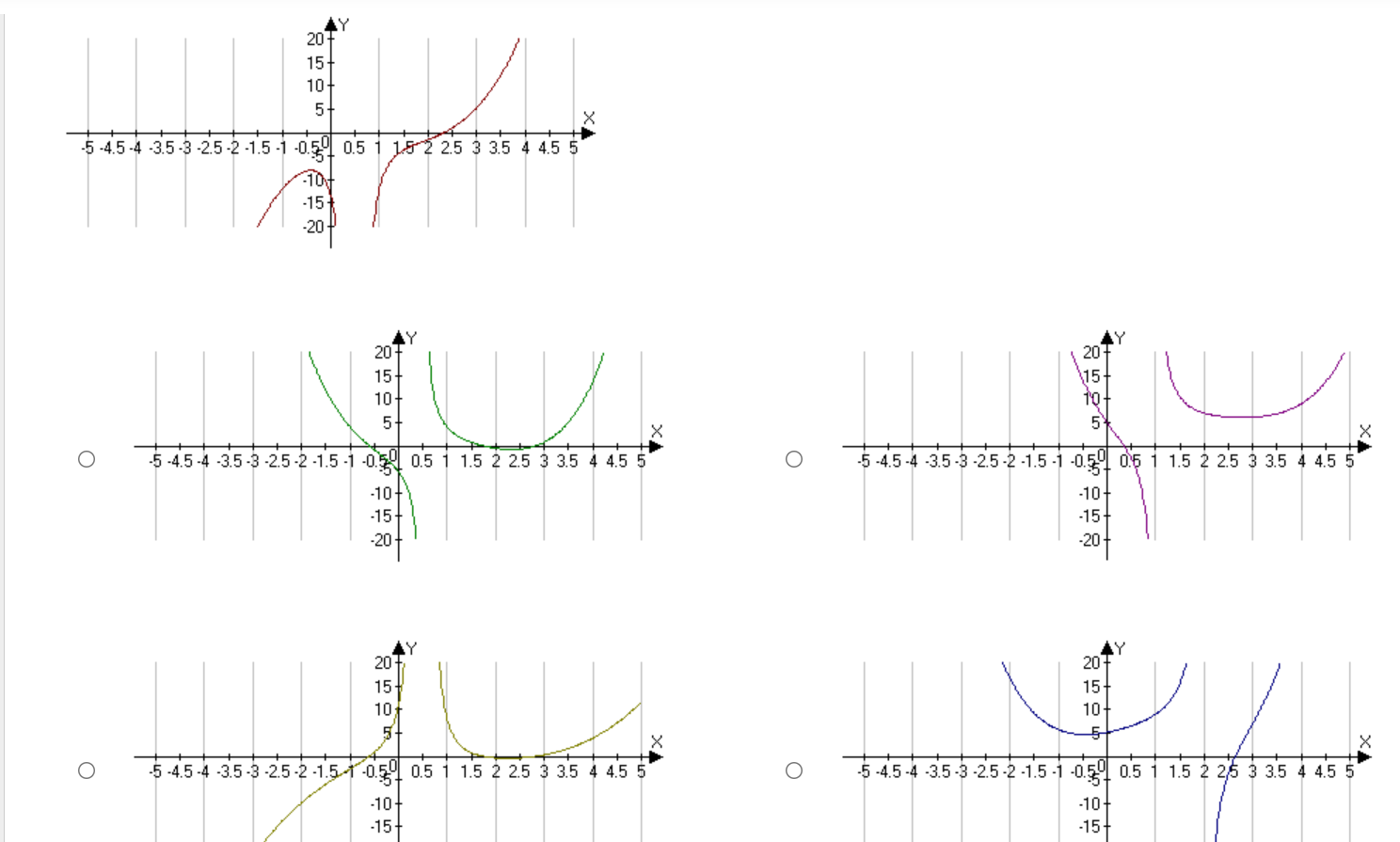
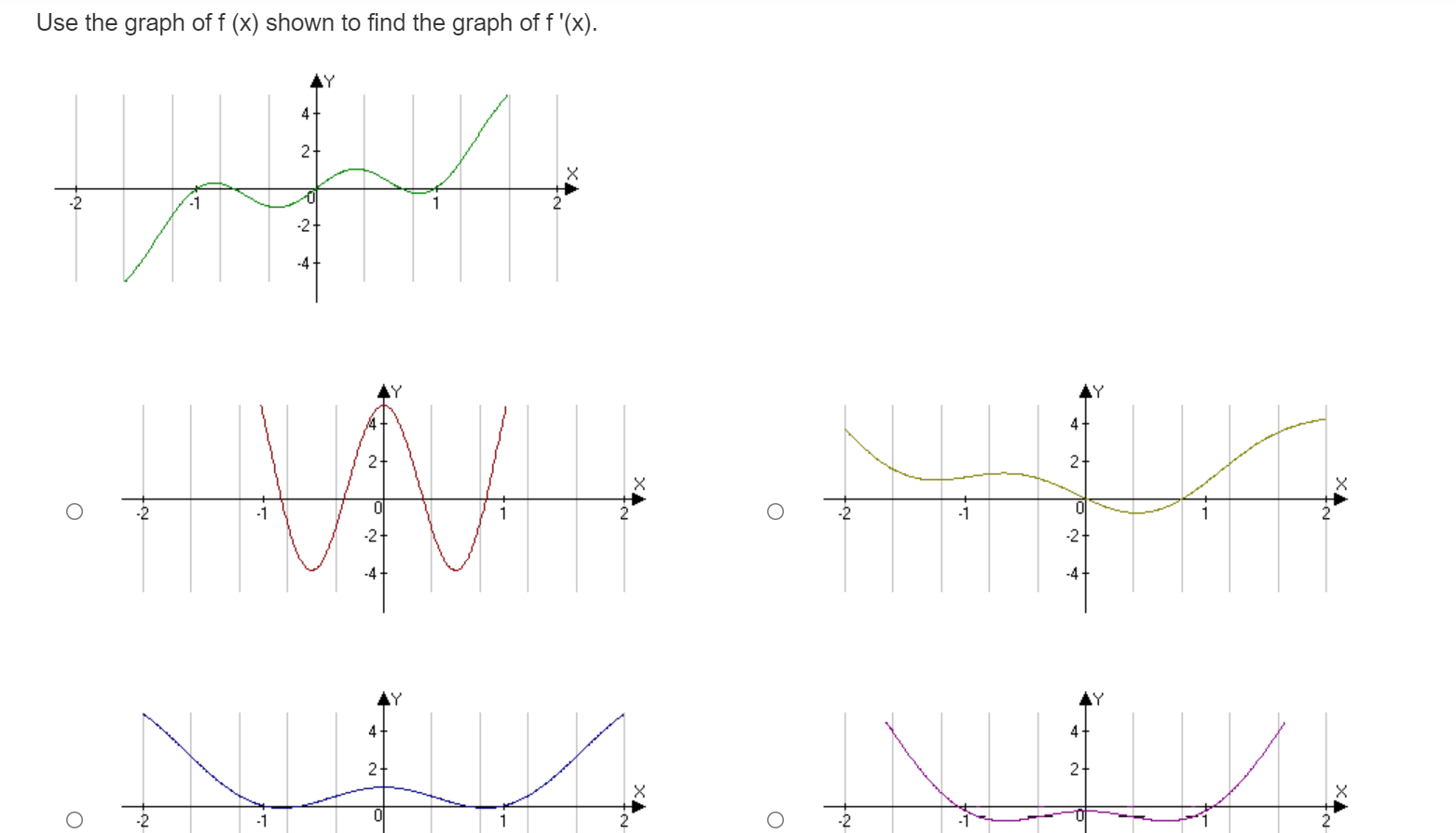
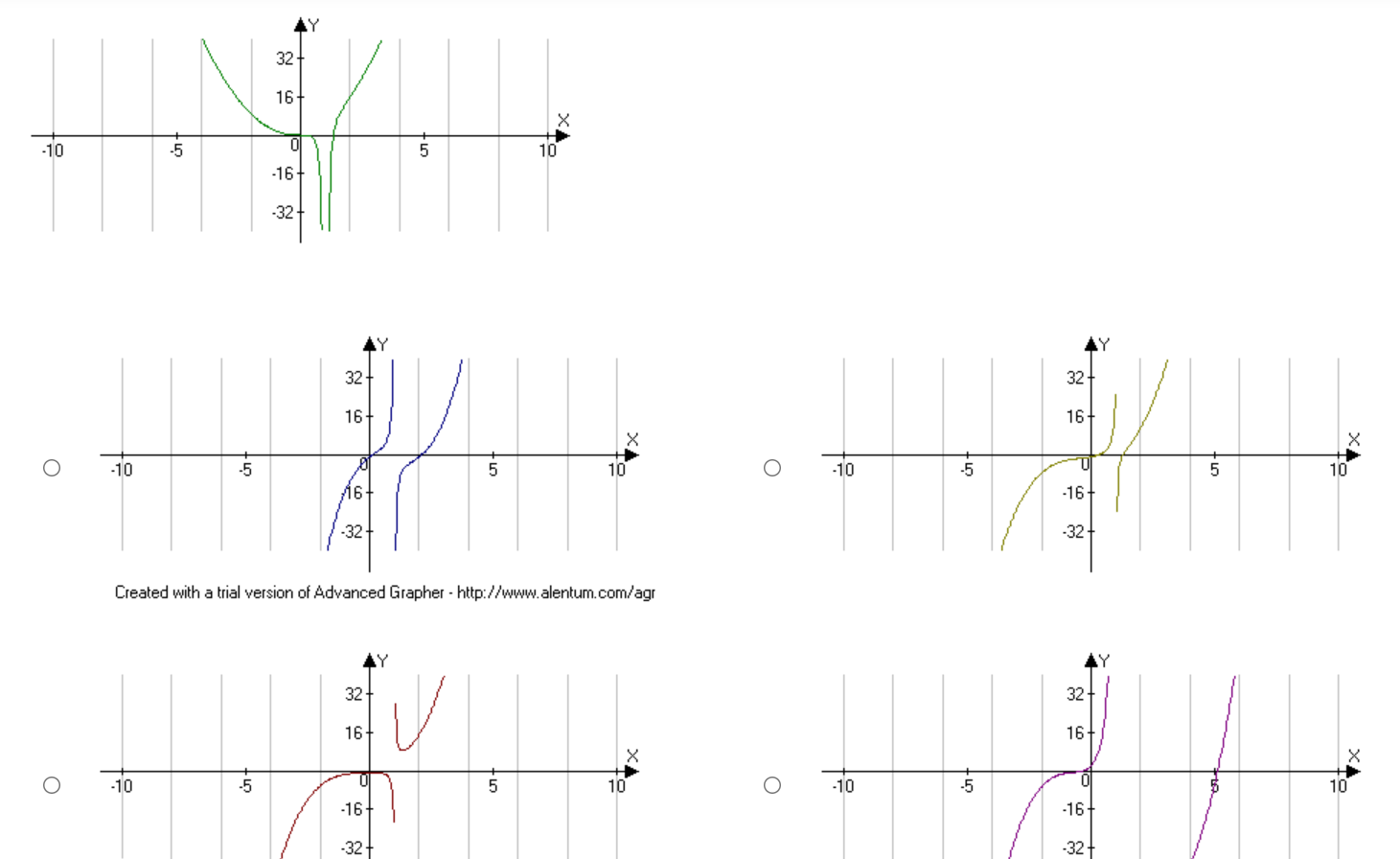
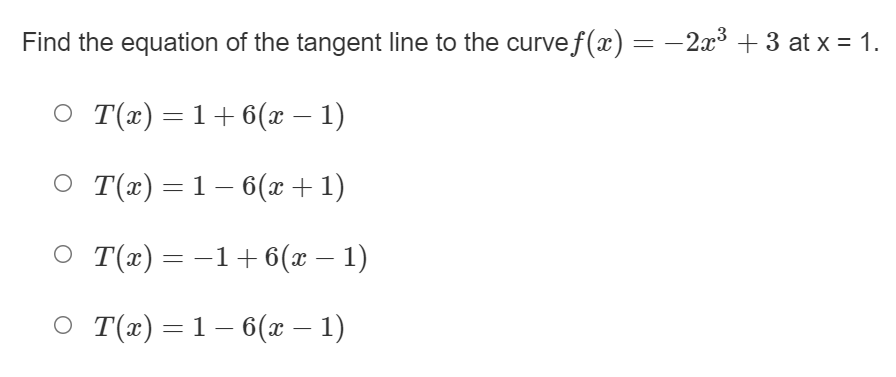
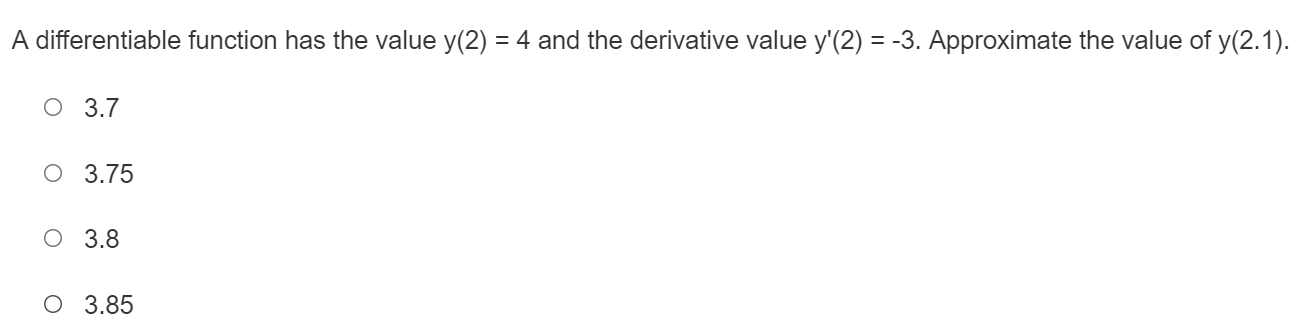
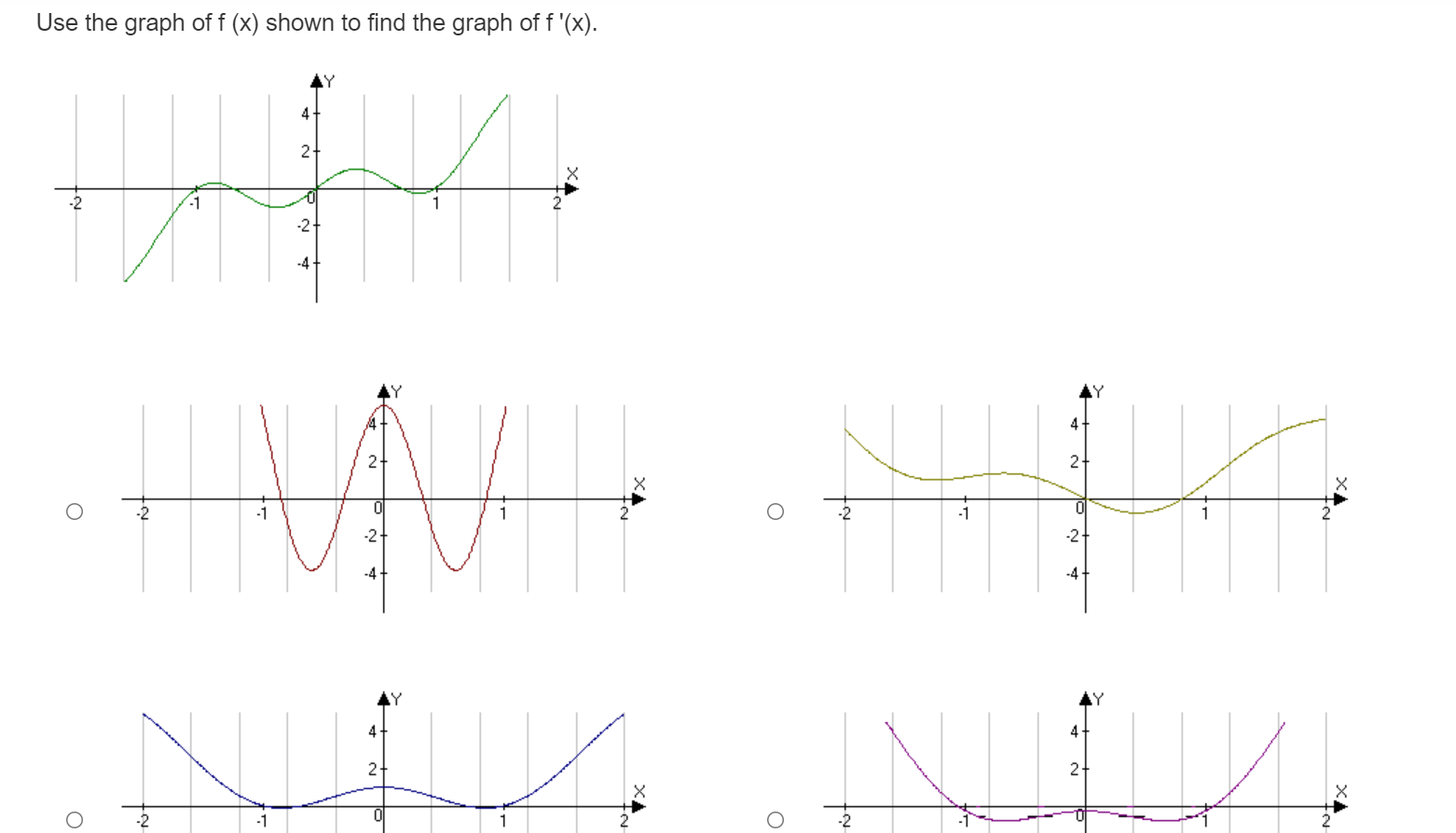
32 + 16+ X -10 5 10 -16+ -32 LY 32 + 32 16+ 16- X X O -10 10 O -10 10 16. -16+ -32 -32 Created with a trial version of Advanced Grapher - http://www.alentum.com/agr LY 32 + 32 + 16+ 16+ X O -10 -5 5 10 O -10 -5 10 -16+ -16 32 32Find the equation of the tangent line to the curvef(:1:) : m2 3:1: at a: : 1. Enter the answer in the box. T(m) : E Find the equation of the tangent line to the curve f (ac) = a + 3 at x = 1. Enter the answer in the box. T(a) =Find the equation of the tangent line to the curvef(:c) : $2 + 1 at x = 0. Use a tangent line approximation to estimate the value of 4.2. Enter the answer in the box. Round the answer to two decimal places. Find the equation of the tangent line to the curve f(ac) = -2x3 + 3 at x = 1. O T(x) = 1+6(x -1) O T(a) =1 -6(x + 1) O T(a) = -1+6(x -1) O T(x) = 1 -6(x - 1)Use a tangent line approximation to estimate the value of x/ 8.8. Enter the answer in the box. Round the answer to four decimal places. A differentiable function has the value y(2) = 4 and the derivative value y'(2) = -3. Approximate the value of y(2. 1). O 3.7 O 3.75 O 3.8 O 3.85\fUse the graph of f (x) shown to find the graph of f'(x). -2 X -2- O -2 X N O X 2- O -2 2- Not O -2 X Not