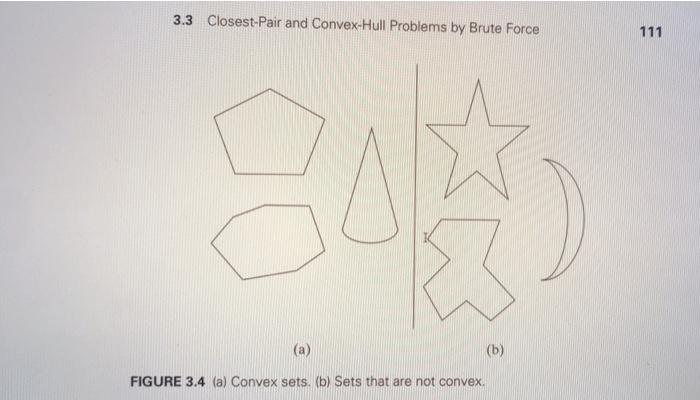
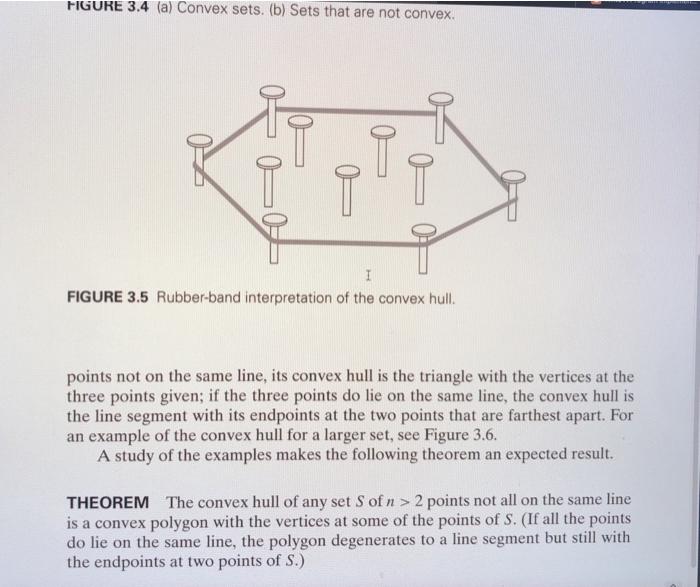
3.3 Closest-Pair and Convex-Hull Problems by Brute Force 111 E (a) (b) FIGURE 3.4 (a) Convex sets. (b) Sets that are not convex. FIGURE 3.4 (a) Convex sets. (b) Sets that are not convex. I FIGURE 3.5 Rubber band interpretation of the convex hull. points not on the same line, its convex hull is the triangle with the vertices at the three points given; if the three points do lie on the same line, the convex hull is the line segment with its endpoints at the two points that are farthest apart. For an example of the convex hull for a larger set, see Figure 3.6. A study of the examples makes the following theorem an expected result. THEOREM The convex hull of any set S of n > 2 points not all on the same line is a convex polygon with the vertices at some of the points of S. (If all the points do lie on the same line, the polygon degenerates to a line segment but still with the endpoints at two points of S.) 112 Brute Force and Exhaustive Search pe P2. P3 ps Pi FIGURE 3.6 The convex hull for this set of eight points is the convex polygon with vertices at Pu Ps. Po pz. and p3. The convex-hull problem is the problem of constructing the convex hull for a given set S of n points. To solve it, we need to find the points that will serve as the vertices of the polygon in question. Mathematicians call the vertices of such a polygon "extreme points." By definition, an extreme point of a convex set is a point of this set that is not a middle point of any line segment with endpoints in the set. For example, the extreme points of a triangle are its three vertices, the extreme points of a circle are all the points of its circumference, and the extreme points of the convex hull of the set of eight points in Figure 3.6 are pl. ps. Po P. and p3 T. and p3 Extreme points have several special properties other points of a convex set do not have. One of them is exploited by the simplex method, a very important algorithm discussed in Section 10.1. This algorithm solves linear programming problems, which are problems of finding a minimum or a maximum of a linear function of n variables subject to linear constraints (see Problem 12 in this section's exercises for an example and Sections 6.6 and 10.1 for a general discussion), Here, however, we are interested in extreme points because their identification solves the convex-hull problem. Actually, to solve this problem completely, we need to know a bit more than just which of n points of a given set are extreme points of the set's convex hull: we need to know which pairs of points need to be connected to form the boundary of the convex hull. Note that this issue can also be addressed by listing the extreme points in a clockwise or a counterclockwise order. So how can we solve the convex-hull problem in a brute-force manner? If you do not see an immediate plan for a frontal attack, do not be dismayed: the convex- hull problem is one with no obvious algorithmic solution. Nevertheless, there is a simple but inefficient algorithm that is based on the following observation about line segments making up the boundary of a convex hull: a line segment connecting two points p, and p, of a set of n points is a part of the convex hull's boundary if and Write a program implementing the brute-force algorithm for the convex-hull problem as described on pages 111 and 112 (Section 3.3) of your textbook. Begin with the bottom-most point and specify the points in counter-clockwise order. In implementing your program, read in the input as shown (the first line is the number of points n, and the remaining n lines contain the x and y coordinates of point i). Assume all coordinates are integers: SAMPLE INPUT: 6 4 17 4 14 7 15 5 13 2 10 57 Your output will consist of a m lines, where m is the number of convex hull points in the format shown: SAMPLE OUTPUT: (5, 7) (7, 15) (4, 17) (2, 10)