Question: 4 . 1 . 2 . Problem. Let S be any set. ( 1 ) Construct an infective map :Slongrightarrow 2 S . ( 2
Problem. Let be any set.
Construct an infective map :Slongrightarrow
Prove that there is no bijection :Slongrightarrow from to
Remark For the proofs,
You need to deal with the case separately.
Since there is an injection :Slongrightarrow but there is no bijection :Slongrightarrow we see that ##
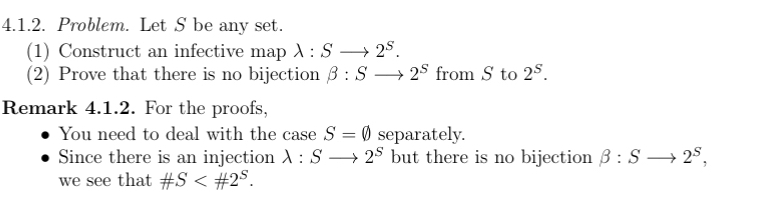
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


