Python please

onku where it says class ADSockDrawer(object)

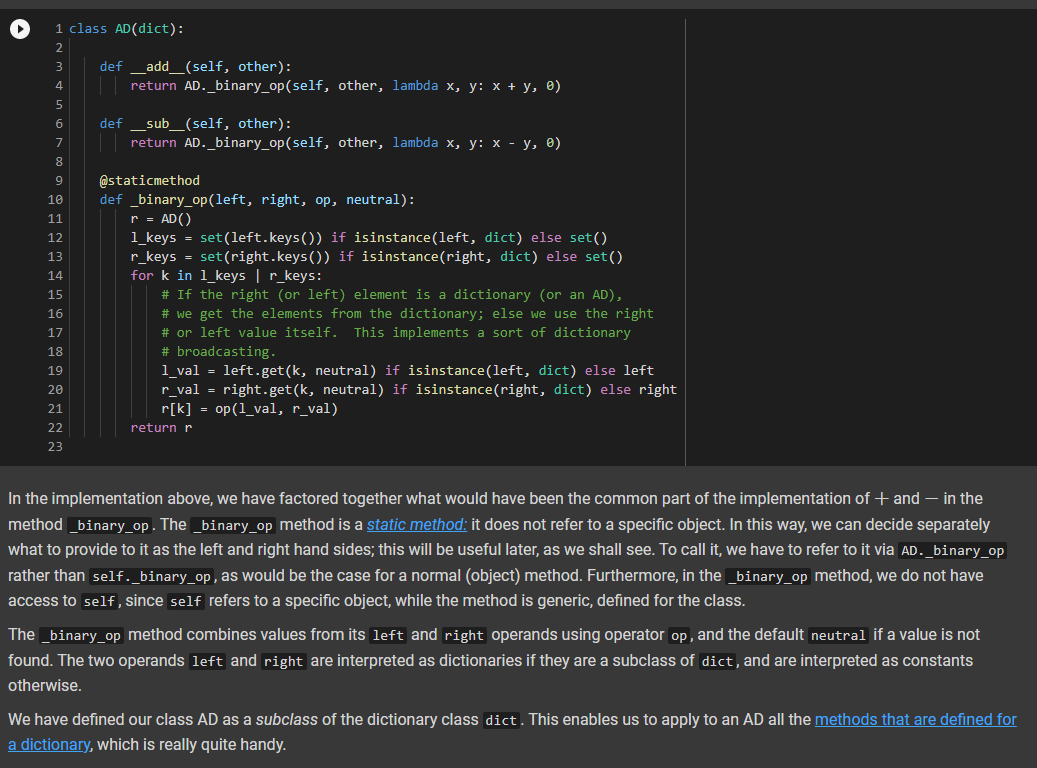
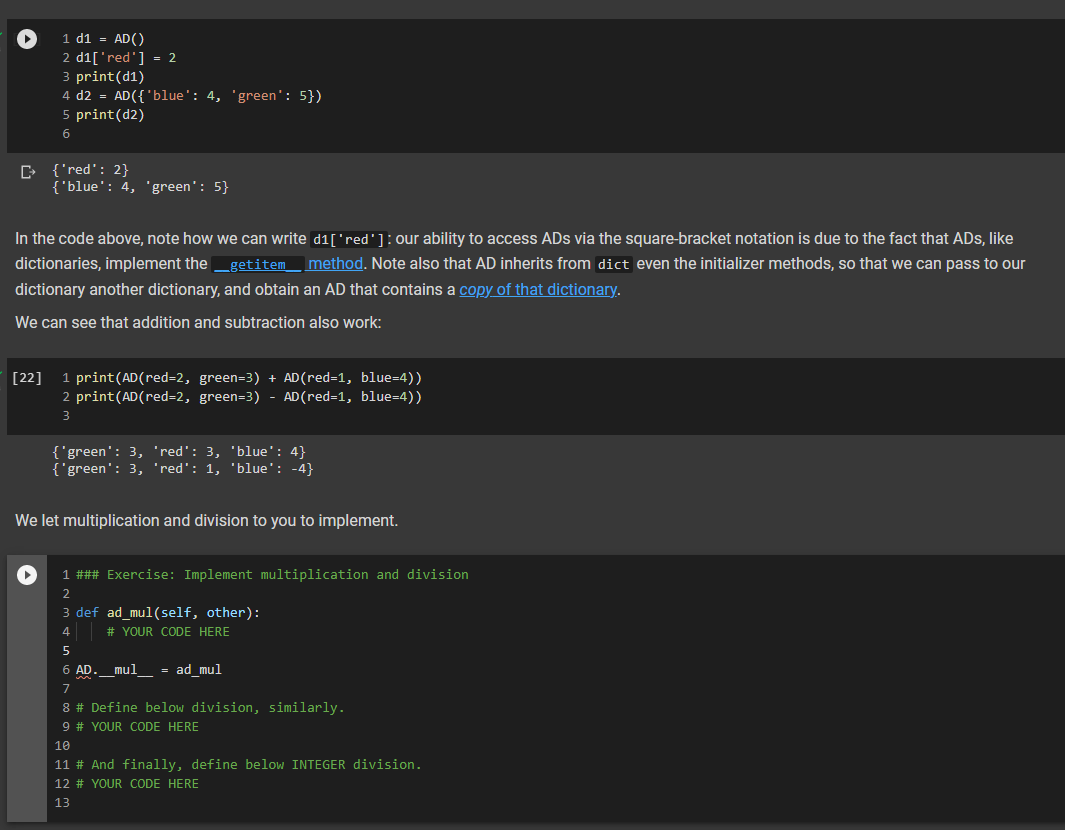
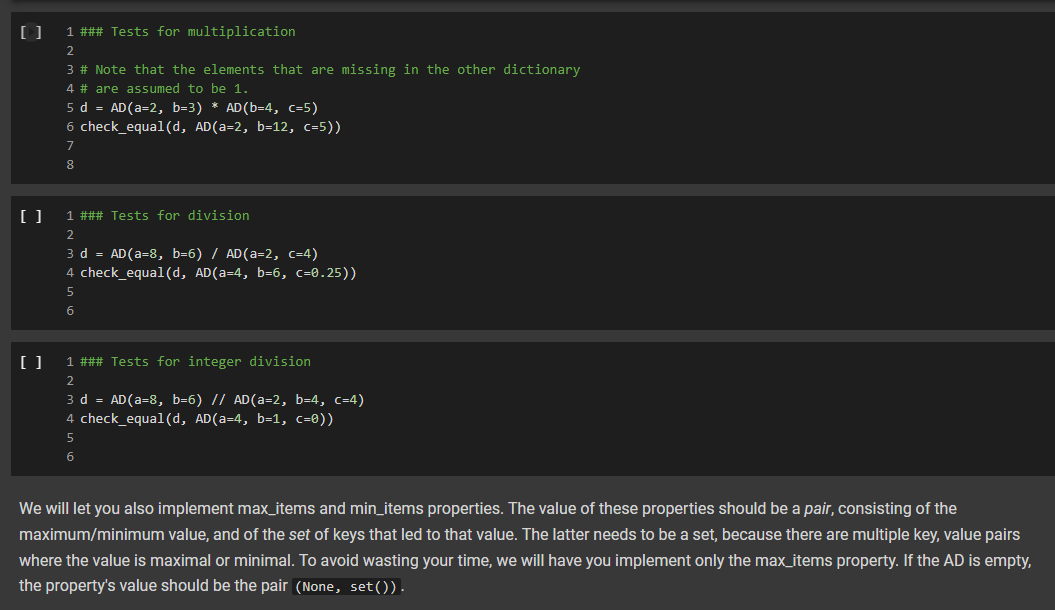
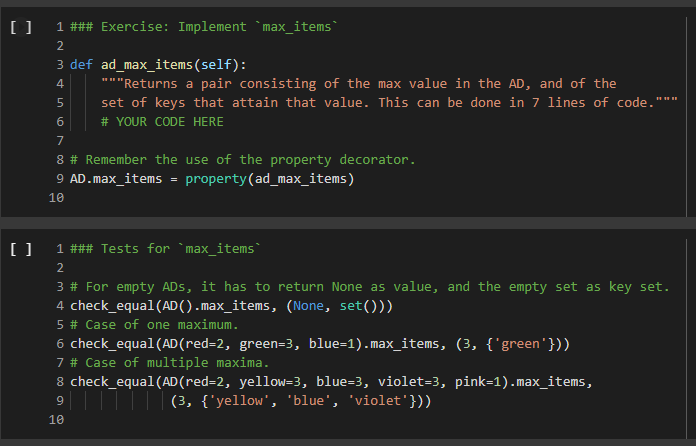
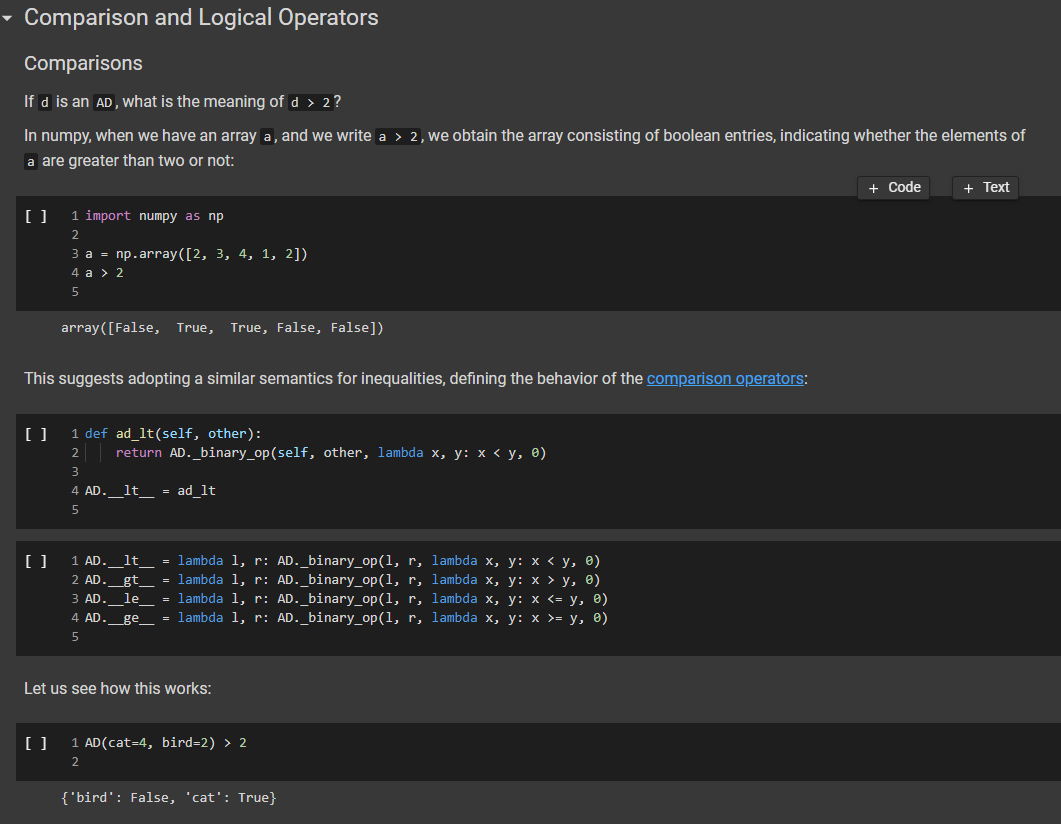
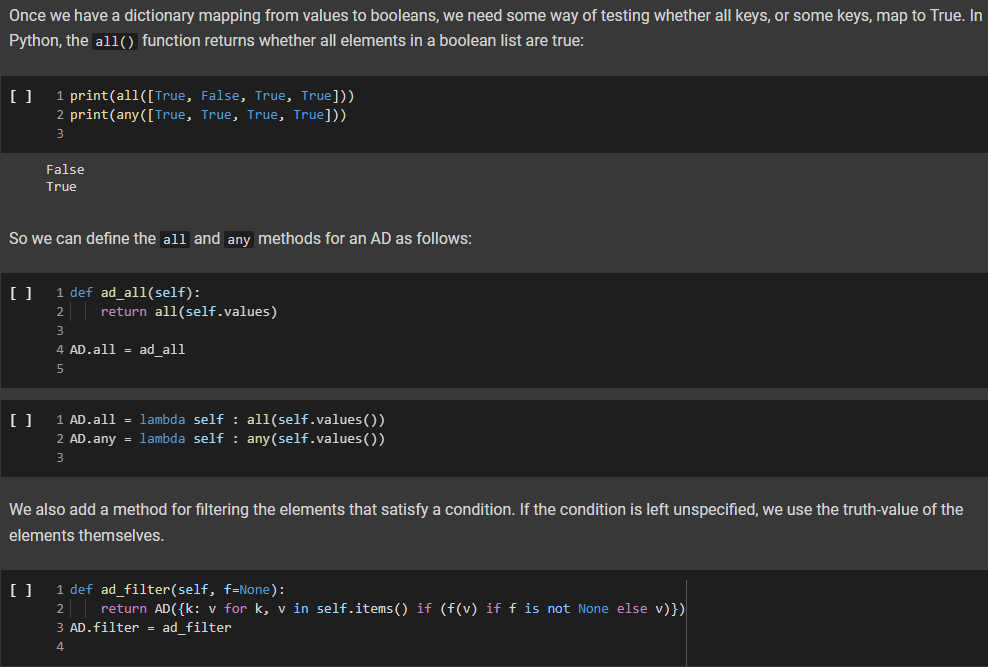
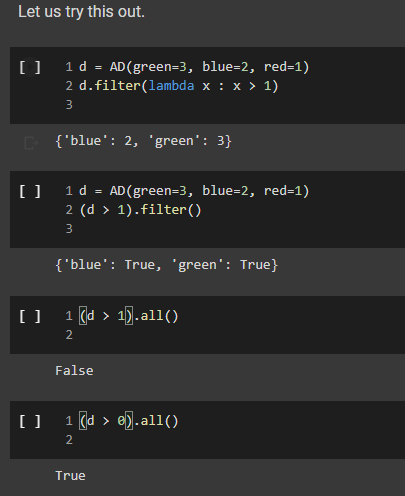
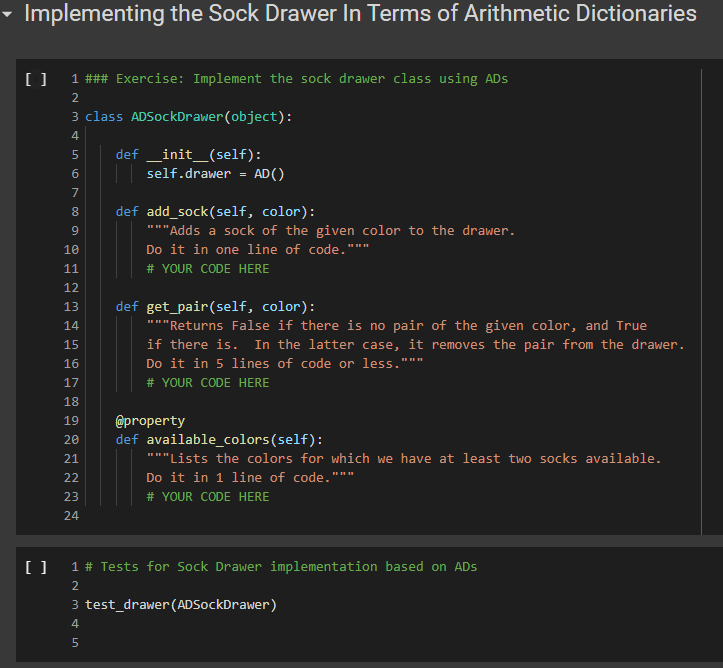
3 1 class AD (dict): 2 def _add_(self, other): 4 | return AD._binary_op(self, other, lambda x, y: x + y, e) 5 def sub_(self, other): 7 return AD._binary_op(self, other, lambda x, y: x - y, ) 6 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 @staticmethod def _binary_op(left, right, op, neutral): r = AD() 1_keys = set(left keys()) if isinstance(left, dict) else set() r_keys = set(right.keys()) if isinstance(right, dict) else set() for k in 1_keys | r_keys: # If the right (or left) element is a dictionary (or an AD), # we get the elements from the dictionary: else we use the right # or left value itself. This implements a sort of dictionary # broadcasting 1_val = left.get(k, neutral) if isinstance(left, dict) else left r_val = right.get(k, neutral) if isinstance(right, dict) else right r[k] = op(1_val, r_val) return r In the implementation above, we have factored together what would have been the common part of the implementation of + and in the method _binary_op. The _binary op method is a static method: it does not refer to a specific object. In this way, we can decide separately what to provide to it as the left and right hand sides, this will be useful later, as we shall see. To call it, we have to refer to it via AD._binary op rather than self._binary_op, as would be the case for a normal (object) method. Furthermore, in the _binary op method, we do not have access to self, since self refers to a specific object, while the method is generic, defined for the class. The _binary op method combines values from its left and right operands using operator op, and the default neutral if a value is not found. The two operands left and right are interpreted as dictionaries if they are a subclass of dict, and are interpreted as constants otherwise. We have defined our class AD as a subclass of the dictionary class dict. This enables us to apply to an AD all the methods that are defined for a dictionary, which is really quite handy. 1 d1 = AD() 2 d1['red'] = 2 3 print(1) 4 d2 = AD({ 'blue': 4, 'green': 5}) 5 print(d2) 6 [{'red': 2} {'blue': 4, 'green': 5} In the code above, note how we can write d1['red']: our ability to access ADs via the square-bracket notation is due to the fact that ADs, like dictionaries, implement the _getitem_method. Note also that AD inherits from dict even the initializer methods, so that we can pass to our dictionary another dictionary, and obtain an AD that contains a copy of that dictionary. We can see that addition and subtraction also work: [22] 1 print(AD(red=2, green=3) + AD(red=1, blue=4)) 2 print(AD(red=2, green=3) - AD(red=1, blue=4)) 3 {'green': 3, 'red': 3, 'blue': 4} {'green': 3, 'red': 1, 'blue': -4} We let multiplication and division to you to implement. 1 ### Exercise: Implement multiplication and division 2 3 def ad_mul(self, other): 4 # YOUR CODE HERE 5 6 AD _mul_ = ad_mul 7 8 # Define below division, similarly. 9 # YOUR CODE HERE 10 11 # And finally, define below INTEGER division. 12 # YOUR CODE HERE 13 [] 1 ### Tests for multiplication 2 3 # Note that the elements that are missing in the other dictionary 4 # are assumed to be 1. 5 d = AD(a-2, b=3) * AD (b=4, C=5) 6 check_equal(d, AD(a=2, b=12, C=5)) 7 8 [ 1 ### Tests for division 2 3 d = AD(a=8, b=6) / AD(a=2, C-4) 4 check_equal(d, AD(a=4, b=6, C=0.25)) 5 6 [] 1 ### Tests for integer division 2 3 d = AD(a=8, b=6) // AD(a=2, b=4, (+4) 4 check_equal(d, AD(a=4, b=1, C=8)) 5 6 We will let you also implement max_items and min_items properties. The value of these properties should be a pair, consisting of the maximum/minimum value, and of the set of keys that led to that value. The latter needs to be a set, because there are multiple key, value pairs where the value is maximal or minimal. To avoid wasting your time, we will have you implement only the max_items property. If the AD is empty, the property's value should be the pair (None, set()). [] HE 1 ### Exercise: Implement max_items 2 3 def ad_max_items(self): 4 **** "Returns a pair consisting of the max value in the AD, and of the set of keys that attain that value. This can be done in 7 lines of code." # YOUR CODE HERE 7 8 # Remember the use of the property decorator. 9 AD.max_items = property(ad_max_items) 10 N m n o N 00 5 6 [] 1 ### Tests for 'max_items 2 3 # For empty ADs, it has to return None as value, and the empty set as key set. 4 check_equal(AD() .max_items, (None, set())) 5 # Case of one maximum. 6 check_equal (AD (red=2, green=3, blue=1).max_items, (3, {'green'})) 7 # Case of multiple maxima. 8 check_equal(AD (red=2, yellow=3, blue=3, violet=3, pink=1).max_items, 9|||TI| (3, {'yellow', 'blue', 'violet'})) 10 Comparison and Logical Operators Comparisons If d is an AD, what is the meaning of d > 2? In numpy, when we have an array a, and we write a > 2, we obtain the array consisting of boolean entries, indicating whether the elements of a are greater than two or not: + Code + Text [] 1 import numpy as np 2 3 a = np.array([2, 3, 4, 1, 2]) 4 a > 2 5 array([False, True, True, False, False]) This suggests adopting a similar semantics for inequalities, defining the behavior of the comparison operators: [] 1 def ad_lt(self, other): 2 return AD._binary_op(self, other, lambda x, y: x y, e) 3 AD. le = lambda 1, r: AD._binary_op(1, r, lambda x, y: x = y, o) 5 Let us see how this works: [] 1 AD(cat=4, bird=2) > 2 2 {'bird': false, 'cat': True} Once we have a dictionary mapping from values to booleans, we need some way of testing whether all keys, or some keys, map to True. In Python, the all() function returns whether all elements in a boolean list are true: [] 1 print(all([True, False, True, True])) 2 print(any ([True, True, True, True])) 3 False True So we can define the all and any methods for an AD as follows: [] 1 def ad_all(self): 2 return all(self.values) 3 4 AD.all = ad_all 5 [] 1 AD.all = lambda self : all(self.values()) 2 AD.any = lambda self : any(self.values()) 3 We also add a method for filtering the elements that satisfy a condition. If the condition is left unspecified, we use the truth-value of the elements themselves. [] 1 def ad_filter(self, f=None): 2 return AD({k: v for k, v in self.items() if (f(v) if f is not None else v)}) 3 AD.filter = ad_filter 4 Let us try this out ( 10 = AD(green=3, blue=2, red=1) 2 d.filter(lambda x : x > 1) 3 D{'blue': 2, 'green': 3} = [ 1 d = AD(green=3, blue=2, red=1) 2 (d > 1).filter() 3 {'blue': True, 'green': True} > 0 1 (ld > 1).all() 2 False ( 1 [ld > 0).all() 2 True - Implementing the Sock Drawer In Terms of Arithmetic Dictionaries [ 1 ### Exercise: Implement the sock drawer class using ADS 2 3 class ADSockDrawer(object): 4 5 def _init__(self): self.drawer = AD() = 6 7 8 00 9 def add_sock(self, color): "***"Adds a sock of the given color to the drawer. Do it in one line of code."" # YOUR CODE HERE 10 11 12 13 14 15 def get_pair(self, color): **"Returns False if there is no pair of the given color, and True if there is. In the latter case, it removes the pair from the drawer. Do it in 5 lines of code or less." # YOUR CODE HERE 16 17 18 19 20 21 @property def available_colors(self): ***"Lists the colors for which we have at least two socks available. Do it in i line of code. "*" # YOUR CODE HERE 22 23 24 [] 1 # Tests for Sock Drawer implementation based on ADs 2 3 test_drawer (ADSockDrawer) 4 5