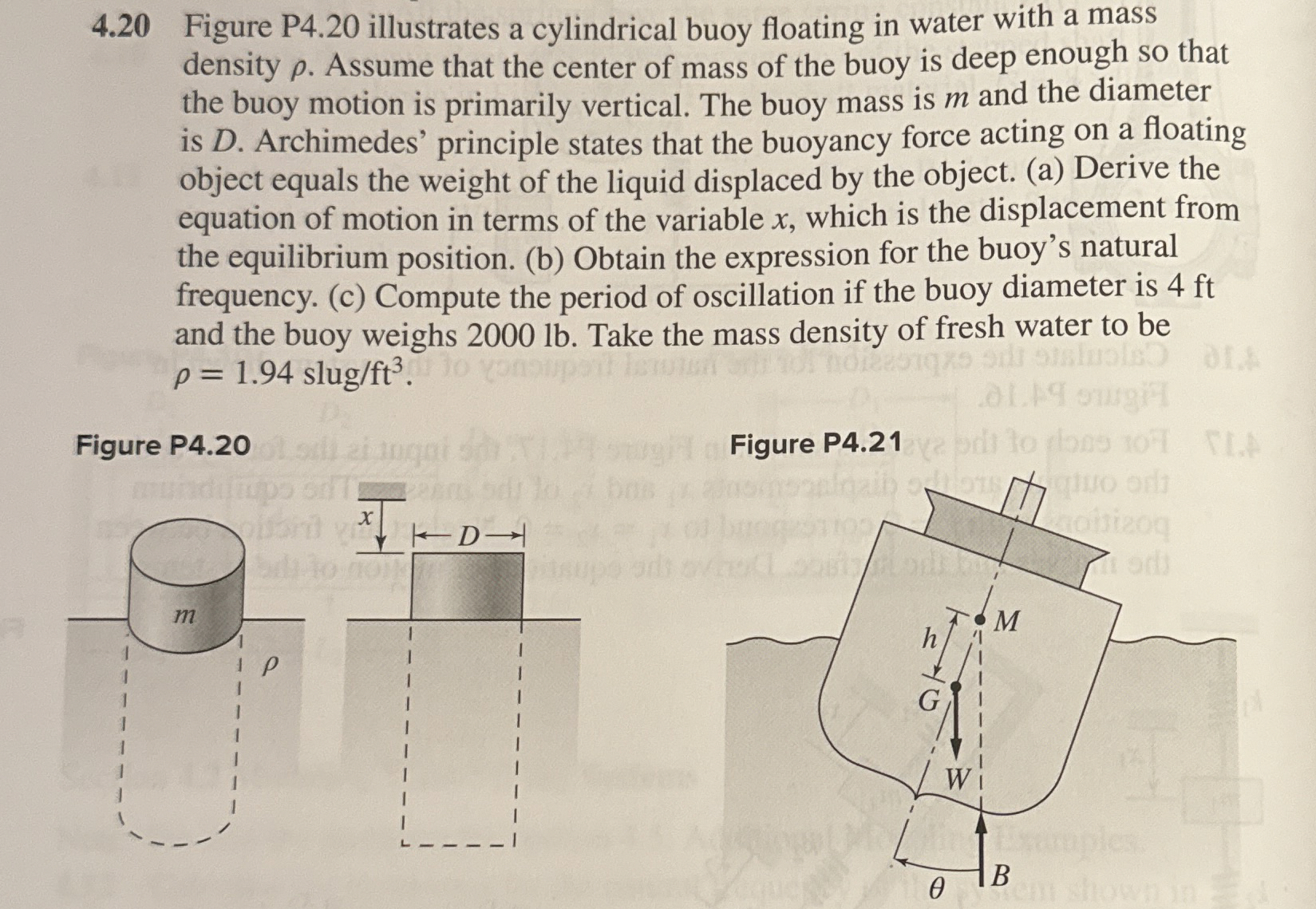
Question: 4 . 2 0 Figure P 4 . 2 0 illustrates a cylindrical buoy floating in water with a mass density . Assume that the
Figure P illustrates a cylindrical buoy floating in water with a mass
density Assume that the center of mass of the buoy is deep enough so that
the buoy motion is primarily vertical. The buoy mass is and the diameter
is Archimedes' principle states that the buoyancy force acting on a floating
object equals the weight of the liquid displaced by the object. a Derive the
equation of motion in terms of the variable which is the displacement from
the equilibrium position. b Obtain the expression for the buoy's natural
frequency. c Compute the period of oscillation if the buoy diameter is ft
and the buoy weighs lb Take the mass density of fresh water to be
slug
Figure P
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


