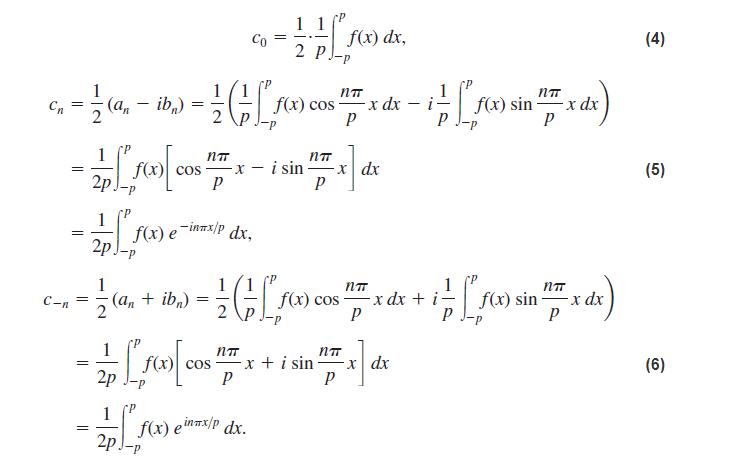
4. (4 pts.) A 2x-periodic function f(x) has the Fourier series expansion f(x) ~ 1+2 ) e"" cos(ni). The complex Fourier series expansion of f(c) is then given by: ( A ) f ( x ) = Cengiz n=0 Solution. (B) f(x) ~ 1+ en ginr f(x) ~1+2) en 2 n=-DO n=1 =1telex + en -ins (C) f(x) = ) ell eins n=1 n=1 n ing m=1 - (D) f(x) ~ e Ingin n=-DO 71= -00 = [ e-Inleinz (E) f(x) ~ 1/2+ e In pine 71=-DO\fComplex Fourier Series If we first add the two expressions in (1) and solve for cos x and then subtract the two expressions and solve for sin x, we arrive at COS X = and Sin x = (2) 2 2i Using (2) to replace cos(nix/p) and sin(nix/p) in (8) of Section 12.2, the Fourier series of a function f can be written do ,innx/P + -innx/p innx/P _ pinax/p + M an + bn 1 = 2 2i = do + 2 (an - ibn)einux/P + 2 - Can + ib )e -inax/p (3) = Co + E cheinmap + Ec_ne -inax/p, 1 = n= where co = - ao, Cn = = (an - ibn), and c-n = = (an + ibn). The symbols ao, an, and by are the coefficients (9), (10), and (11) respectively, in Definition 12.2.1. When the function fis real, Cn and con are complex conjugates and can also be written in terms of complex exponential functions:\f